Опр. Сверткой функций f 1(t) и f 2(t) наз. интеграл от произведения этих функций 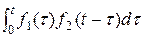
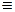 f 1(t)* f 2(t). Перестановка функций не меняет значения свертки.
f 1(t)* f 2(t). Перестановка функций не меняет значения свертки.
Теорема о свертке Изображение свертки двух оригиналов равно произведению их изображений, т.е. если f 1(t) =: F 1(p), f 2(t) =: F 2(p), то
f 1(t)* f 2(t) =: F 1(p) F 2(p) (14)
Доказательство. Обе части формулы преобразований Лапласа F 1(p) = 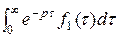 умножим на F 2(p): F 1(p) F 2(p) =
умножим на F 2(p): F 1(p) F 2(p) = 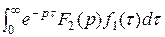 . По теореме запаздывания (4)
. По теореме запаздывания (4) 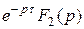 =: f 2(t -
=: f 2(t - 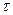 ) или
) или 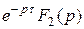 = =
= =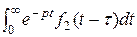 , где t >
, где t > 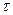 . Тогда F 1(p) F 2(p) =
. Тогда F 1(p) F 2(p) = 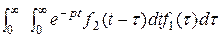 =
=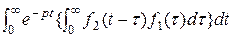 =:
=: 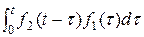 ,т.к. при
,т.к. при 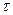 > t f 2(t -
> t f 2(t - 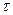 ) = 0 по 10 свойству оригинала.
) = 0 по 10 свойству оригинала.
Пр.17 Найти оригинал изображения F (p) = 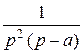 .
.
Решение 1. Имеем произведение изображений двух функций t и eat. Поэтому оригинал равен свертке этих функций f (t) = t* eat =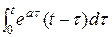 = t
= t 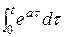 -
- 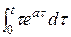 = J 1 - J 2,
= J 1 - J 2,
J 1 = t 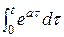 = t
= t 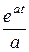 -
- 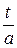 ; J 2 =
; J 2 = 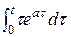 =
= 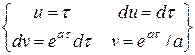 =
=
= 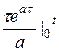 -
- 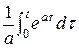 = t
= t 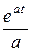 -
- 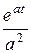 +
+ 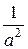 . Ответ f (t) =
. Ответ f (t) = 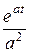 -
- 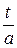 -
- 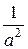 .
.
Решение 2. Представим изображение в виде суммы простейших дробей: F (p) =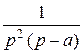 =
=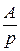 +
+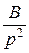 +
+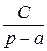 , тогда Ap (p – a) + B (p – a) + Cp 2 = 1
, тогда Ap (p – a) + B (p – a) + Cp 2 = 1
p 2 | A + C = 0 A = - 1/ a 2
p 1 | - aA + B = 0 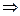 B = -1/ a По формулам № 1, 2, 3 получаем оригинал
B = -1/ a По формулам № 1, 2, 3 получаем оригинал
p 0 | - aB = 1 C = 1/ a 2 f (t) = -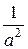 -
- 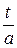 +
+ 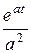
 2014-01-24
2014-01-24 1144
1144








