Дифференцирование оригиналов и изображений

Теорема о дифференцировании оригинала Пусть оригинал f (t) и его производная f ` (t) имеют одинаковый показатель роста s _0,тогда их изображения имеют простую алгебраическую связь

f `(t) =: p F (p) - f (0)(7)

Доказательство.

f `(t) =: = ==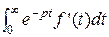

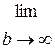
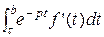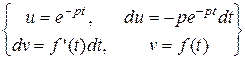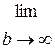= [ f (t) e^-pt |₀ ^b + p 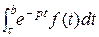] = p F (p) - f (0) + 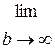f (b) e^-pb,

но последнее слагаемое обращается в 0, т.к. Re p = s > s ₀.

Пр.14 Найти изображение cos t с учетом равенства cos t = (sin t)`

cos t = (sin t)` =: p 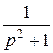- sin 0 =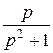

Вычислим изображение 2 производной оригинала по формуле (7)

f ``(t) =: p [ pF (p) - f (0) ] - f `(0) = p <sup>2</sup> F (p) – p f (0) – f ` (0) (8)

Переходя к производным высших порядков, получаем общую формулу

f ^{( n )}(t) =: pⁿ F (p) - p^{n – 1 f} (0) - p^{n – 2 f} `(0) -... - f ^{( n – 1)}(0), Re p > s ₀ (9)

Теорема о дифференцировании изображения Дифференцирование изображения приводит к оригиналу, который отличается от исходного оригинала только общим множителем - t:

F` (p) =: - tf (t)(10)

К (10) приводит дифференцирование по p левой и правой части равенства (1). Повторные дифференцирования дают формулу

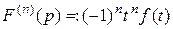.(11)

Пр.15 Найти изображение для t sin at, t cos at, t e^at.

Т.к. sin at умножается на t, то достаточно продифференцировать его изображение

t sin at =: - (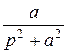)` = 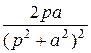(формула № 10)

t cos at =: - (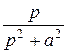)` = 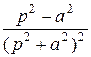(формула № 9)

t e^at =: - ( 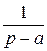)` = 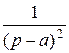(формула № 8)