2014-01-24
764
При решении системы ЛДУ с постоянными коэффициентами для каждой неизвестной функции вводится свое изображение и решение задачи сводится к решению системы алгебраических уравнений для изображений.
Рассмотрим систему двух ЛДУ 1 порядка
x` (t) + a 11 x (t) + a 12 y (t) = f 1(t) (18)
y` (t) + a 21 x (t) + a 22 y (t) = f 2(t)
при начальных условиях x (0) = x 0, y (0) = y 0. Функции f 1(t), f 2(t) оригиналы.
Пусть x (t) =: F 1(p), у (t) =: F 2(p), f 1(t) =: Ф 1(p), f 2(t) =: Ф 2(p). Построим изображающее уравнения с учетом формулы (6), т.е. x` (t) =: pF 1(p) - x 0, y` (t) =: pF 2(p) - y 0
pF 1(p) - x 0 + a 11 F 1(p) + a 12 F 2(p) = Ф 1(p) (19)
pF 2(p) - y 0 + a 21 F 1(p) + a 22 F 2(p) = Ф 2(p)
Из решения системы находят F 1(p), F 2(p), а затем их оригиналы x (t), y (t).
Пр.21 При условии x (0) = y (0) = 0решить систему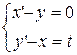 
.
Т.к. t =: 1/ p 2(Пр.5), то система (18) принимает вид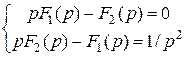 
Решение системы F 1(p) =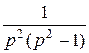
; F 2(p) =
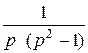. Эти изображения разложим на сумму простейших дробей: F 1(p) = - 
+ 
- 
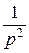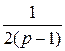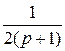, F 2(p) = - 
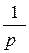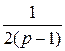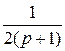+ +и по формулам № 1, 3 перейдем к оригиналам, которые дают решение исходной системы уравнений:
x (t) = – t + ½ et – ½ e-t, y (t) = – 1 + ½ et + ½ e-t.
Проверка. x` (t) – у (t) = [– 1 + ½ et + ½ e-t ] – [– 1 + ½ et + ½ e-t ] = 0
|
|
|
у` (t) – x (t) = [½ et – ½ e-t ] – [– t + ½ et – ½ e-t ] = t
