2014-01-24
978
Теорема об интегрировании оригинала. Интегрирование оригинала приводит к делению изображения на параметр p
=: 
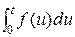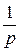F (p) (12)
Доказательство. Интеграл 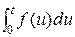удовлетворяет всем 3 условиям, опреде-ляющим оригинал. Обозначим 
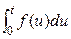= Ф (p), тогда по формуле (7) имеем
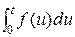()` = pФ (p) - 
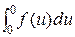= pФ (p),
но интеграл с переменным верхним пределом является первообразной для подынтегральной функции и производная от него есть подынтегральная
функция, т.е. f (t) =: pФ (p) или Ф (p) =: 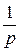F (p).
Пр.16 Найти изображение для f (t) = tn.
Интеграл от единичной функции 
( t ) дает t. Последующие интегри-рования приведут к функции tn / n!. При каждом интегрировании изображе-ние F (p) =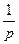
умножится на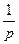
=: = 
; 
= 
=: 
;
= 
=: 
; 
= 
=: 
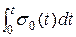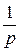
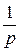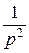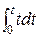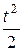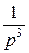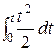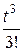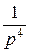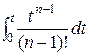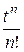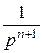
В результате получим формулу № 2 из таблицы tn =: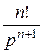 
.
Теорема об интегрировании изображения Интегрирование изображения от p до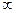 
приводит к делению оригинала на переменную t
=: 
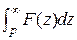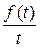, (13)
где F (z) аналитическая функция.
