2014-01-24
696
Основные свойства преобразования Лапласа
Определение 1. Ф ункция f (t), определенная для всех значений действительного переменного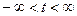 
, называется изображаемой по Лапласу или оригиналом, если она удовлетворяет следующим условиям:
1) при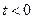 
, 
,
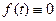2) при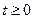 
, f (t) на любом конечном участке 
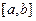положительной полуоси t удовлетворяет условиям Дирихле: а) ограничена, б) либо непрерывна, либо имеет лишь конечное число точек разрыва первого рода, в) имеет конечное число экстремумов,
3) при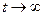 
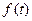имеет ограниченную степень роста, т.е. существуют такие положительные постоянные М > 0 и 
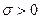, что для всех 
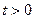модуль функции 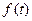растет не быстрее некоторой показательной функции:
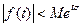, (1)
величина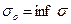 
(точная нижняя грань тех значений 
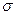, для которых имеет место данное неравенство) называется показателем степени роста или показателем роста функции f (t).
