1) f (t) может быть комплексной функцией действительного переменного t: f (t) = f 1(t) + if 2(t), где f 1(t) и f 2(t) – действительные функции.
2) Умножение f (t) на любую степенную функцию вида 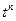 не меняет ее степени роста.
не меняет ее степени роста.
3) Функции вида 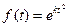 ,
, 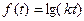 ,
, 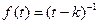 (k > 0) не могут рассматриваться в операционном исчислении, поскольку для них неравенство (1) не может быть выполнено для всех
(k > 0) не могут рассматриваться в операционном исчислении, поскольку для них неравенство (1) не может быть выполнено для всех 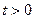 ни при каких постоянных М и
ни при каких постоянных М и 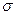 .
.
4) 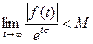
Определение 2. Преобразованием Лапласа заданной функции 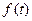 действительного переменного t, которая может принимать и комплексные значения, называется преобразование, ставящее в соответствие функции
действительного переменного t, которая может принимать и комплексные значения, называется преобразование, ставящее в соответствие функции 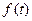 функцию F (p) комплексного переменного р, определенную с помощью интеграла:
функцию F (p) комплексного переменного р, определенную с помощью интеграла:
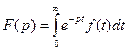 . (2)
. (2)
Данный интеграл называется интегралом Лапласа, а определяемая им функция F (p) называется образом или лапласовым изображением функции f (t) или просто изображением функции f (t).
Соответствие между оригиналом f (t) и его изображением F (p) символически записывается в виде: 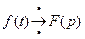 ,
, 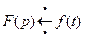 или
или 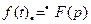 (3)
(3)
Уславливаются за значение оригинала f (t) во всякой его точке разрыва I рода t 0 принимать полусумму его предельных значений слева и справа от этой точки: 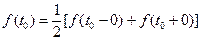 при
при 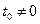 ;
; 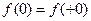 при t 0 = 0. При соблюдении этого условия соответствие между оригиналами и изображениями взаимно однозначно, т.е. всякому оригиналу соответствует единственное изображение и обратно.
при t 0 = 0. При соблюдении этого условия соответствие между оригиналами и изображениями взаимно однозначно, т.е. всякому оригиналу соответствует единственное изображение и обратно.
Несобственный интеграл 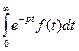 зависит от переменного р = α + iβ как от параметра и сходится не при всех значениях р, например, если
зависит от переменного р = α + iβ как от параметра и сходится не при всех значениях р, например, если 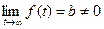 , а
, а 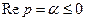 , то интеграл расходится. Следовательно, стоит вопрос о сходимости интеграла и области определения F (p).
, то интеграл расходится. Следовательно, стоит вопрос о сходимости интеграла и области определения F (p).
Теорема 1. Интеграл 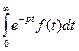 сходится абсолютно в области
сходится абсолютно в области 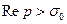 , где
, где 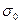 – показатель степени роста f (t), причем в области
– показатель степени роста f (t), причем в области 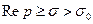 этот интеграл сходится равномерно.
этот интеграл сходится равномерно.
(без доказательства)
Замечание. Сходимость интеграла обеспечивает условие (1).
Теорема 2. Изображение Лапласа F (p) является аналитической функцией в полуплоскости 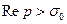 , где
, где 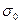 – показатель степени роста оригинала f (t).
– показатель степени роста оригинала f (t).
Лемма 1. Пусть функция f (t) действительного переменного t определена для всех 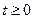 , и пусть существует такое комплексное число p 0 , что сходится интеграл
, и пусть существует такое комплексное число p 0 , что сходится интеграл 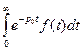 , тогда для всех р, удовлетворяющих условию
, тогда для всех р, удовлетворяющих условию 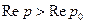 , сходится и интеграл Лапласа
, сходится и интеграл Лапласа 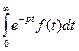 .
.
(без доказательства)
Этой леммой расширили класс функций f (t), допускающих преобразование Лапласа. В качестве основного класса функций f (t), для которых строится преобразование Лапласа, рассматриваются функции, удовлетворяющие условию леммы.
Область определения F (p). С помощью преобразования (2) функция F (p) определена в полуплоскости комплексной плоскости (р) правее прямой 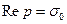 , параллельной мнимой оси, т.е. в области
, параллельной мнимой оси, т.е. в области 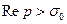 .
.
Не всякая функция F (p) является изображением некоторой функции. Например, не существует оригинала для функции tg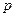 , так как полюсы тангенса расположены на всей вещественной прямой, а не справа от некоторой прямой
, так как полюсы тангенса расположены на всей вещественной прямой, а не справа от некоторой прямой 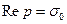 .
.
Лемма 2. 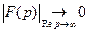 . (без доказательства)
. (без доказательства)
Замечание. В практических приложениях часто пользуются преобразованием Хевисайда:
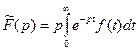 . (4)
. (4)
Области определения функций 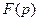 и
и 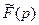 совпадают.
совпадают.
 2014-01-24
2014-01-24 713
713








