2014-01-25
904
Общий вид дифференциального уравнения I порядка:
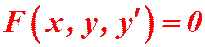(1)
Если уравнение (1) можно разрешить относительно производной, то его можно переписать: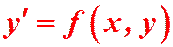 
(2)
Определение. Функция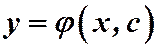 
, дифференцируемая по 
и непрерывная по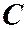 
, где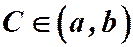 
, называется общим решением уравнения (1), если выполняются условия:
1) для любого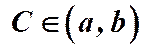 
эта функция является решением (1);
2) когда 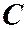пробегает весь интервал 
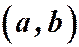, мы получаем все решения данного уравнения.
Определение. Частным решением уравнения (1) называется любое его решение, которое получается из общего решения при фиксированном .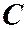
Геометрический смысл общего и частного решений
Пусть функция 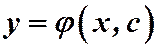есть общее решение уравнения (1). Зафиксируем 
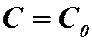, тогда получим функцию одного переменного 
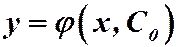. График этой функции называется интегральной кривой. Если 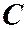изменить, то получим семейство интегральных кривых.
Вернемся к задачам 1) и 2) и построим интегральные кривые:
1) 
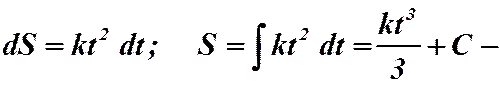общее решение дифференциального уравнения.
При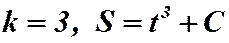 
, задавая 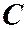, получим кубические параболы следующего вида:
2) 
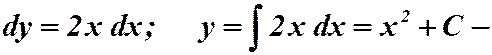общее решение дифференциального уравнения.
|
|
|
Замечание. Не всегда при интегрировании решение дифференциального уравнения получается в явном виде.
Чаще всего, это решение имеет
вид: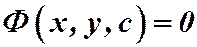 
и называется общим интегралом данного дифференциального уравнения.
4. Задача Коши
Решив задачу 1), мы получили закон движения при 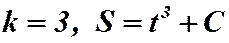. Но с точки зрения физики этот закон неопределенный, т.к. он содержит 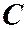– произвольную постоянную. Чтобы окончательно определить закон движения, нужно наложить условия на 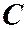. Например, при 
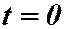пусть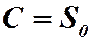 
. Тогда закон 
.
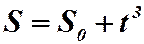Таким образом, мы пришли к задаче с начальным условием.
Задача Коши:
Пусть дано дифференциальное уравнение: 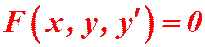(1)
и два числа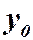 
и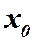 
, которые мы будем называть начальными данными. Требуется найти решение 
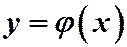уравнения (1), удовлетворяющее начальному условию: 
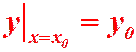или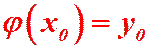 
.
Геометрический смысл задачи Коши заключается в том, что интегральная кривая проходит через точку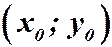 
.
Пример.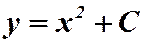 
. Пусть 
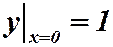. Уравнение с начальными условиями – это задача Коши.
Решение.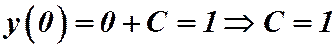 
. Получим частное решение – решение задачи Коши. 
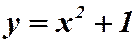, которая проходит через точку 
.
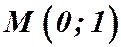Теорема о существовании и единственности задачи Коши. Если функция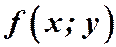 
непрерывна и имеет непрерывные частные производные 
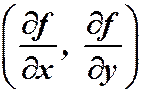в области 
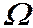, то существует единственное решение 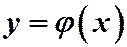уравнения (1), удовлетворяющее заданному начальному условию 
.
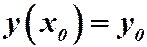Геометрический смысл этой теоремы в том, что через каждую точку области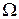 
проходит единственная интегральная кривая.
