Уравнения с разделяющимися переменными
Простейшие типы дифференциальных уравнений I порядка
Определение. Дифференциальное уравнение называется уравнением с разделенными переменными, если в нем коэффициент при 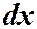 зависит только от
зависит только от 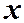 , а при
, а при 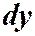 зависит только от
зависит только от 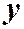 . Общий вид:
. Общий вид: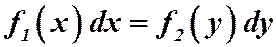 . Далее проинтегрировав, получим решение:
. Далее проинтегрировав, получим решение: 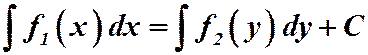 .
.
Пример 1-2.
1) 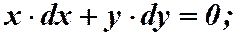
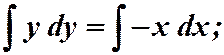
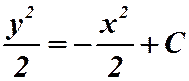 ;
;
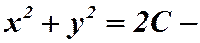 общий интеграл (концентрические окружности).
общий интеграл (концентрические окружности).
2) 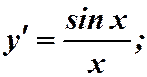
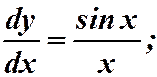
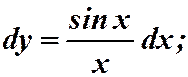
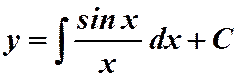 .
.
Интеграл справа не берется в конечном виде. В этом случае говорят, что уравнение проинтегрировано в квадратурах.
Определение. Квадратурой называется взятие неопределенного интеграла в уравнении.
Уравнение является интегрированным в конечном виде, если его общий интеграл выражается через элементарные функции или квадратуры.
Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение, в котором коэффициенты при 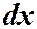 и
и 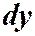 распадаются на множители только от одной переменной.
распадаются на множители только от одной переменной.
Общий вид: 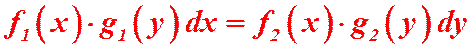 .
.
Используя правило умножения и деления, разделив на 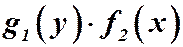 , получим уравнение с разделенными переменными:
, получим уравнение с разделенными переменными: 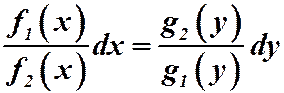 .
.
Замечание. Здесь предполагается, что 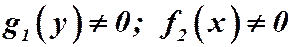 .
.
Пример 2. 1) 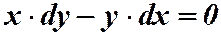 . Разделяя дифференциалы:
. Разделяя дифференциалы:
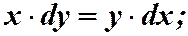
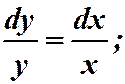
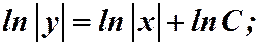
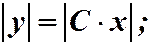
 .
.
2) 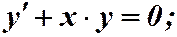
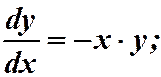
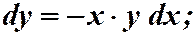
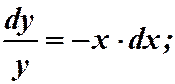
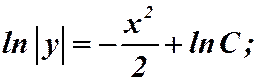
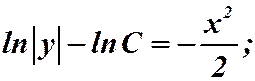
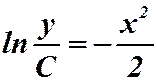 ;
; 
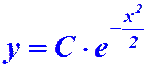 .
.
Определение. Функция 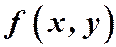 называется однородной функцией k -го измерения, если при замене в ней
называется однородной функцией k -го измерения, если при замене в ней 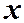 на
на 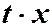 , а
, а 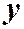 на
на 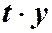 выполняется равенство:
выполняется равенство: 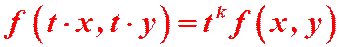 .
.
Пример 1. 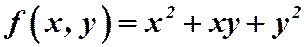 .
.
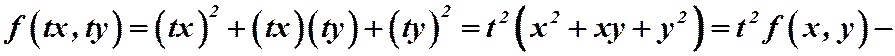 т.е. функция второго измерения. Если
т.е. функция второго измерения. Если 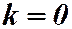 , то получаем однородную функцию нулевого измерения, т.е. имеет место равенство:
, то получаем однородную функцию нулевого измерения, т.е. имеет место равенство:
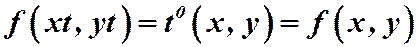 при любом
при любом 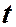 . Положим
. Положим 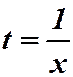 , получим:
, получим:
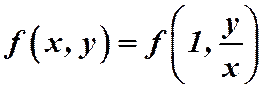 .
.
Это говорит о том, что однородную функцию нулевого измерения можно представить как функцию отношения 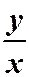 , т.е.
, т.е. 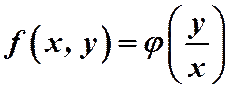 .
.
Определение. Уравнение 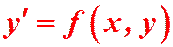 называется однородным, если его правая часть есть однородная функция нулевого измерения.
называется однородным, если его правая часть есть однородная функция нулевого измерения.
Общее решение однородного уравнения находится с помощью подстановки 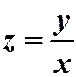 , где
, где 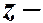 новая переменная, зависящая от
новая переменная, зависящая от 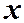 , т.е.
, т.е. 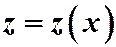 .
.
Однородное уравнение перепишем в виде: 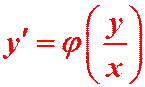 (1)
(1)
Из замены 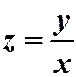 следует:
следует: 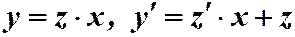 .
.
Подставляя замену в уравнение (1), получаем:
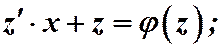
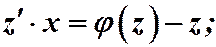
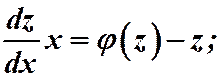
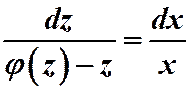 ;
; 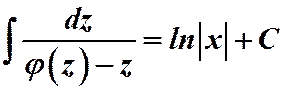 .
.
Таким образом, однородное уравнение с помощью подстановки 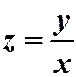 всегда приводится к уравнению с разделяющимися переменными.
всегда приводится к уравнению с разделяющимися переменными.
Пример 2. Решить уравнение: 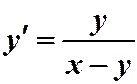 .
.
Решение. 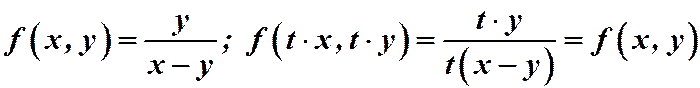 .
.
Имеем однородную функцию нулевого измерения. Замена: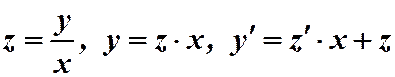 . Подставляем в уравнение:
. Подставляем в уравнение:
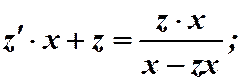
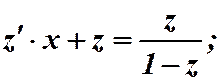
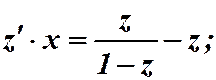
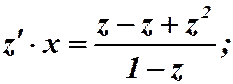
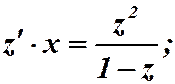
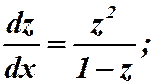
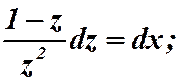
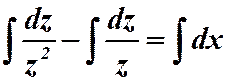 ;
; 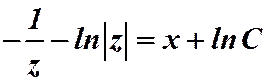
Возвращаясь к замене:
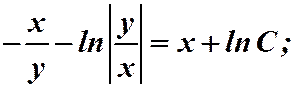
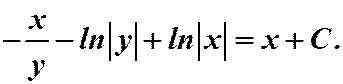
Однородное уравнение можно записать в дифференциальной форме:
 (общий вид),
(общий вид),
где 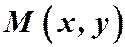 и
и 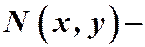 однородные функции одного измерения.
однородные функции одного измерения.
Пример 3. 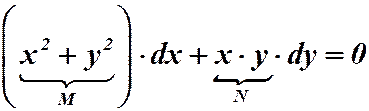 . М и N – это функции второго измерения, следовательно, уравнение однородное. Делаем замену:
. М и N – это функции второго измерения, следовательно, уравнение однородное. Делаем замену:
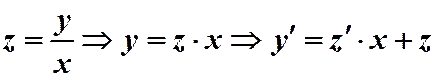 . Здесь лучше найти
. Здесь лучше найти 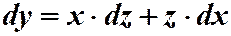 .
.
Подставляем: 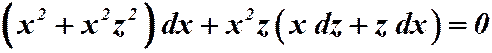 .
.
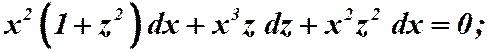
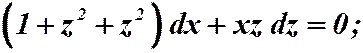
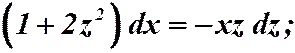
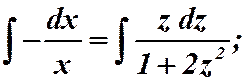
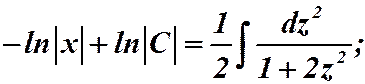
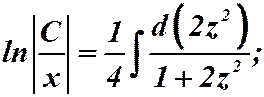
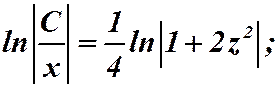

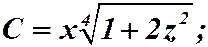
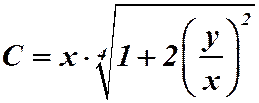 .
.
 2014-01-25
2014-01-25 765
765








