Взаимное положение двух прямых

Две прямые в пространстве могут пересекаться, скрещиваться и быть параллельными. Однако отсутствие второй проекции не дает возможности определить взаимное расположение прямых непосредственно по чертежу, не проведя предварительно вспомогательных построений. Так взаимное расположение прямых можно определить, если проградуировать прямые и сравнить интервалы, уклоны и отметки точек пересечения проекций прямых. Отметим признаки характерные для различных случаев расположения прямых.

Параллельные прямые – проекции прямых параллельны, уклоны (или интервалы) равны, и числовые отметки возрастают (или убывают) в одном направлении (рис. 14.10). При этом прямые, соединяющие точки с одинаковыми отметками, параллельны. Они являются горизонталями плоскости, проходящей через заданные прямые.

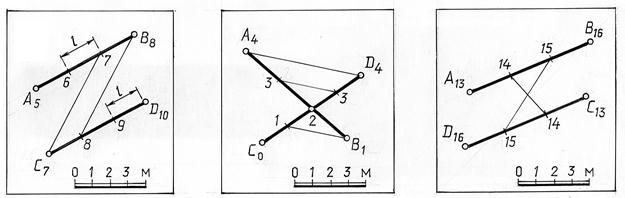
Рис.14.10 Рис.14.11 Рис.14.12

Пересекающиеся прямые – проекции прямых пересекаются в точке, которая, будучи отнесена к каждой из пересекающихся прямых, имеет одинаковую отметку (рис. 14.11). Это легко проверить, если прямые проградуированы. Отметим, что прямые, соединяющие точки с одинаковыми отметками, параллельны. Они являются горизонталями плоскости, проходящей через заданные пересекающиеся прямые.

Скрещивающиеся прямые – прямые, у которых признаки пересечения и параллельности отсутствуют (рис. 14.12). В этом случае прямые, соединяющие точки с одинаковыми отметками, не параллельны.

Пример. Через точку А(А₃) провести горизонтальную прямую, пересекающую заданную прямую СД(С₁Д₇) (рис. 14.13).

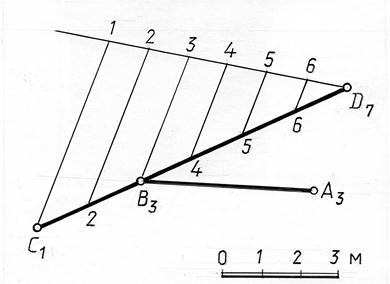
Рис. 14.13

Решение. Искомая горизонтальная прямая определяется точкой А(А₃) и точкой В(В₃) на прямой СD, имеющей такую же отметку.

Проградуируем прямую СD, применяя пропорциональное деление отрезка. Построенную проекцию В₃ соединим с проекцией А₃. Прямая АВ(А₃В₃) – искомая.