Прямая на плоскости. Различные способы задания прямой.
Уравнение прямой с угловым коэффициентом
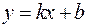 – это уравнение прямой с угловым коэффициентом (1)
– это уравнение прямой с угловым коэффициентом (1)
Если прямая проходит через начало координат, то 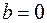 и уравнение
и уравнение 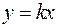 .
.
Если прямая параллельна оси 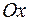 , то
, то 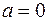 и уравнение
и уравнение 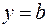 .
.
Уравнение прямой, параллельной оси 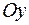 , получается особо. Ясно, что оно:
, получается особо. Ясно, что оно: 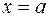 .
.
Общее уравнение прямой
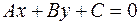 (2)
(2)
Геометрический смысл коэффициентов А и В общего уравнения прямой: упорядоченная пара (-В,А) является координатами направляющего вектора прямой, упорядоченная пара (А,В) является координатами вектора нормали.
Уравнение прямой, проходящей через две заданные точки.
Уравнение прямой, проходящей через точки 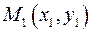 и
и 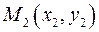 имеет вид
имеет вид 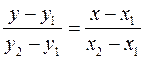 . (3)
. (3)
Уравнение прямой в отрезках
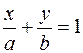 – это уравнение прямой в отрезках. (4)
– это уравнение прямой в отрезках. (4)
Уравнение прямой, проходящей через точку в заданном направлении
Найдем уравнение прямой, не параллельной оси 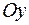 , проходящей через данную точку
, проходящей через данную точку 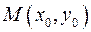 и имеющей заданное направление. Направление прямой можно задать ее угловым коэффициентом
и имеющей заданное направление. Направление прямой можно задать ее угловым коэффициентом 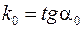 .
.
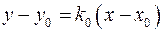 . (5)
. (5)
Пример: через точку 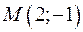 провести прямую перпендикулярную к прямой
провести прямую перпендикулярную к прямой 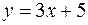 .
.
Решение: из условия перпендикулярности 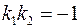 ;
; 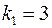 ;
; 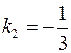 ;
; 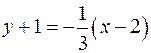 ;
; 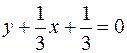 ;
; 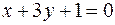 .
.
Уравнение прямой, заданной точкой и вектором нормали.
Точка М0(х0,у0) и ненулевой вектор n(A,B).
A(x-x0)+B(y-y0)=0 – уравнение прямой заданной точкой и вектором нормали. (6)
Каноническое уравнение прямой.
Точка М0(х0,у0) и ненулевой вектор а(а1,а2) – параллелен прямой (называется направляющий вектор).
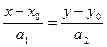 (7)
(7)
Параметрические уравнения прямой
М(х,у) – произвольная точка прямой, М0(х0,у0) – данная точка прямой, ненулевой вектор а(а1,а2) – направляющий вектор этой прямой, t – вещественное число (параметр).
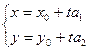
 2014-01-25
2014-01-25 1118
1118








