Лекция 8. Функции, развитие которых необходимо для овладения понятием числа

Как было уже сказано, развитие математического мышления в большой степени зависит от освоения ребенком системы зритель­но-пространственных отношений, что происходит благодаря его действиям с разными предметами. Над проблемой развития поня­тия о числе много работал Пиаже (1965). Математическое мышле­ние — это пространственное мышление. Для усвоения четырех основных видов математических действий — сложения, вычита­ния, умножения и деления — у ребенка должны быть хорошо развиты пространственное представление и мышление. Мы гово­рим о пространстве чисел («10», «20»), о расширении вычисли­тельного пространства. Мы измеряем длину, протяженность, рас­кладываем числа, составляем частичные множества. При этом всегда речь идет об отношениях в пространстве. Пространственное мышление и оперирование им выступают предпосылкой для по­нимания математических операций. Понимание действий с чис­лами зависит в первую очередь от развития трех функций:

- способности классифицировать (классификация);

- способности построения ряда (сериация);

- способности находить соответствия 1:1.

Чтобы классифицировать предметы, ребенок должен уметь вы­являть их сходство и различие и соответственно их группировать. Важной предпосылкой для этого является образование таких по­нятий, как «все красные треугольники». Осознание схожести пред­метов позволяет детям развивать понятия «такой же», «такие же», символизируемые значком =, смысл которого становится теперь ребенку понятен.

Чтобы построить ряд (серию) (рис. 19), ребенок должен владеть способностью подобрать предметы и соотнести их по убывающе­му (возрастающему) признаку (например, разложить в опреде­ленной последовательности предметы, разные по длине). Выпол­нение этих заданий возможно в том случае, если у ребенка хоро­шо развита ориентация в пространстве. Упражнения в составле­нии ряда предметов учат понимать число как выражение величи­ны и порядка. Если ребенок не может построить ряд предметов, то это значит, что у него нарушены вычислительные операции.

Способность устанавливать взаимнооднозначное соответствие является важной предпосылкой для того, чтобы ребенок мог ос­воить понятие «много одинаковых». Выполняя такие задания, ре­бенок учится шаг за шагом узнавать отношения «много одинако­вых — не все одинаковые — меньше, чем — больше, чем». Спо­собность понимать соотношение 1: 1 развивается в возрасте от 4 до 7 лет. Она тесно связана с усвоением количественных значений. При выполнении таких заданий ребенок начинает понимать, что такое вариативность. Благодаря таким действиям, как «дополнить», «доложить», «достроить», у ребенка развивается понимание мате­матических операций сложения или вычитания и формируется представление о величине, связанное с числами.

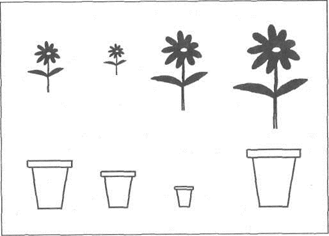
Рис. 19. Построение ряда: какой цветок подходит для какого горшка?