Числовые характеристики дискретных случайных величин

Определение 1 Математическим ожиданием дискретной случайной величины 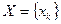называется сумма произведений всех ее возможных значений на их вероятности

.

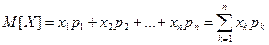Для бесконечной случайной величины: .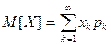

Математическое ожидание обладает следующими свойствами:

1. Математическое ожидание постоянной величины равно этой величине:

M [ C ]= C, где С =const.

2. Числовой множитель можно выносить за знак математического ожидания:

M [ CX ]= C · M [ X ].

3. Математическое ожидание произведения двух независимых случайных величин Х и У равно произведению их математических ожиданий:

М [ XY ]= M [ X ] · M [ Y ].

5.Математическое ожидание суммы двух случайных величин Х и У равно сумме их математических ожиданий: М [ X+Y ]= M [ X ] + M [ Y ].

6.Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:

М (X- M[X])=0.

Математическое ожидание любой случайной величины Х представляет собой среднее арифметическое всех возможных значений этой величины.

Определение 2. Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения значений величины от ее математического ожидания:

.

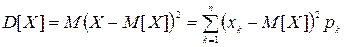Характеристиками рассеивания возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднеквадратичное отклонение.

Среднеквадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:

.

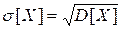Дисперсия обладает следующими свойствами.

1. Дисперсия константы равна нулю: D [ C ]=0, где С =const.

2. При увеличении случайной величины в С раз ее дисперсия увеличится в C ² раз: D [ CX ]= C ²· D [ X ].

3. Дисперсия суммы (разности) двух независимых случайных величин Х и У равна сумме из дисперсий: D [ X+Y ]= D [ X ] + D [ Y ].

4. Дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания: D [ X ]= M [ X ²] – (M [ X ])².