2014-01-25
654
Определение 1. Пусть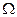 
- вероятностное пространство. Числовая функция X(
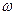), определенная на 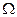называется случайной величиной дискретного типа, если она принимает конечное или счетное множество значений 
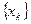, причем множество 
=
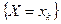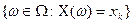являются событиями для всех значений 
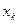величины X().
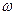Определение 2. Функция f(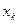)=P(X=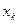) называется законом распределения случайной величины Х.
Последовательность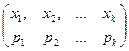 
, где 
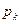= f(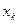) называется рядом распределения случайной величины Х.
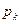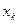График функции = f() называется многоугольником (полигоном) распределения вероятностей.
Определение 3. Две дискретные случайные величины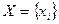 
и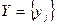 
называются независимыми, если события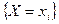 
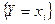являются независимыми при любых 
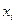и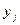 
.
Случайные величины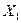 
, 
, …, 
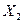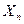(n≥2) называются независимыми, если события 
, 
, …, 
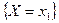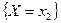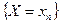независимы в совокупности при любых возможных значениях этих величин.
