2014-01-25
680
Функция распределения случайной величины
Определение 1. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньшее x:
.
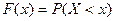Определение 2. Cлучайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
1. Значения функции распределения принадлежат отрезку [0.1]: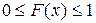 
.
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. если х 1< х 2, то F (x 1)≤ F (x 2).
3. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, в) равна приращению функции распределения на этом интервале:
4. 
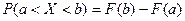
5. Если все возможные значения случайной величины Х находятся на интервале (а, b), то F (x)=0 при х ≤ а и F (x)=1 при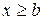 
.
6. 
, 
.
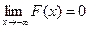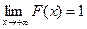Определение. Плотность распределения вероятностей непрерывной случайной величины Х называют функцию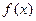 
- первую производную от функции распределения F (x): 
.
|
|
|
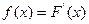Плотность вероятности 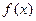существует только для непрерывных случайных величин.
