Теорема 1. Пусть 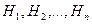 полная группа событий из
полная группа событий из 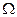 . Тогда для
. Тогда для 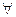 события
события 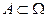 имеет место формула, называемая формулой вероятности:
имеет место формула, называемая формулой вероятности:
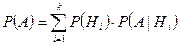 .
.
Доказательство. Так как 
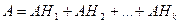 и события
и события 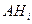 и
и 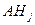 не пересекаются при
не пересекаются при 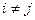 , то
, то
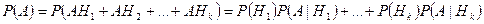 .
.
Пример 1. На продажу в магазин поступили однотипные изделия с двух заводов А и В. С завода А поступило 200 изделий, с завода В 800 изделий. При этом 50% изделий, доставленных с завода А, изготовлены в одном из цехов этого завода, 30% в другом и 20 % в третьем. Брак составляет соответственно 1,5%, 2% и 2,5%. Аналогично, 60% изделий, поступивших с завода В, изготовлено в одном цехе, а 40% - в другом. Брак составляет соответственно 1,5%, 2%. Какова вероятность того, что наугад выбранное изделие является дефектным?
Решение:
Обозначим 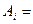 {выбранное изделие принадлежит i- му цеху завода В}, i =1, 2, 3.
{выбранное изделие принадлежит i- му цеху завода В}, i =1, 2, 3.
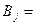 {выбранное изделие принадлежит j-му цеху завода В}, j=1, 2.
{выбранное изделие принадлежит j-му цеху завода В}, j=1, 2.
События 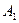 ,
, 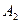 ,
, 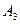 ,
,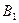 ,
,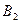 образуют полную группу.
образуют полную группу.
Следовательно, 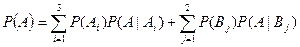 ,
,
где А ={выбранное изделие является дефектным}. Найдем вероятности, входящие в данную формулу.
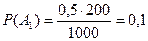 ;
; 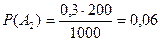 ;
; 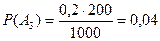 ;
;
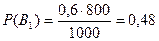 ;
; 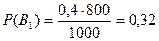 .
.
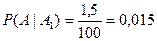 ;
; 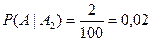 ;
; 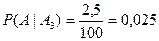 ;
;
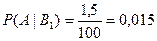 ;
; 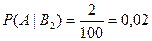 .
.
Следовательно 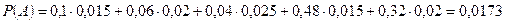 .
.
Пример 2. Из колоды карт последовательно без возвращения вытаскивается 3 карты. Какова вероятность того, что 3-я карта будет тузом, если известно, что первая карта является тузом.
Обозначим 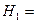 {вторая карта туз},
{вторая карта туз}, 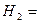 {вторая карта не туз}.
{вторая карта не туз}.
Тогда 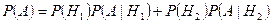 .
.
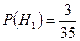 ;
; 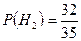 ;
; 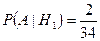 ;
; 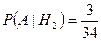 .
.
Следовательно, 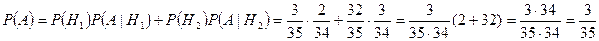 .
.
Теорема 2. Пусть 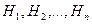 образуют полную группу событий из
образуют полную группу событий из 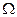 . Тогда имеет место формула Байеса:
. Тогда имеет место формула Байеса:
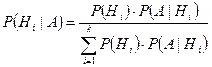 , i =1,..,k.
, i =1,..,k.
Пример 1. Два стрелка независимо друг от друга делают по одному выстрелу по общей мишени. Вероятность попадания в мишень для первого стрелка равна 0,8, а для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что эта пробоина принадлежит первому стрелку?
Обозначим 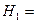 {первый стрелок попадет в мишень },
{первый стрелок попадет в мишень }, 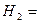 {второй стрелок попадет в мишень}, А={в мишени будет обнаружена одна пробоина}.
{второй стрелок попадет в мишень}, А={в мишени будет обнаружена одна пробоина}.
Имеем, 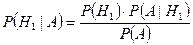 .
.
Так как 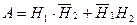 , то
, то 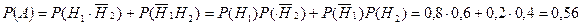
Следовательно с учетом того, что 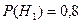 и
и 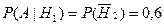 получаем
получаем 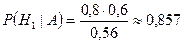 ;
; 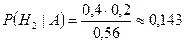 .
.
 2014-01-25
2014-01-25 719
719








