2014-01-25
721
1, Дискретная случайная величина Х имеет биномиальный закон распределения, если она принимает значения 0, 1, 2, …, n с вероятностями
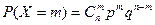m=0,1,…,n, где q=1-p, 0 ≤p≤1. – формула Бернулли.
Теорема1. Математическое ожидание случайной величины Х, распределенной по биномиальному закону равно произведению числа испытаний на вероятность появления события в каждом испытании:
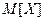= n p.
Теорема 2. Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
D [ X ]= npq.
Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m… с вероятностями:
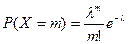(λ>0).
Теорема Пуассона. Закон распределения Пуассона является предельным случаем биномиального закона распределения при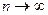 
, 
, 
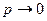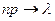, т.е. при всех m=0, 1, 2, … 
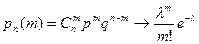при .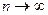
(Так как вероятность p в каждом испытании мала, то закон распределения Пуассона называют законом редких явлений).
Теоремой Пуассона можно пользоваться вместо формулы Бернулли, когда n большое число, p- малое и λ=np≤10.
Математическое ожидание случайной величины Х, распределенной по закону Пуассона, равно: 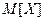= λ.
Дисперсия случайной величины Х, распределенной по закону Пуассона, равна:
D [ X ]= λ.
