Примеры.. Решение. Сравним данный ряд с рядом . Он расходится

1. Исследовать на сходимость .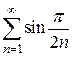

Решение. Сравним данный ряд с рядом 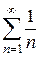. Он расходится.

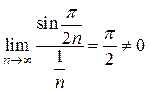. Значит, ряды ведут себя одинаково.

Ответ. Исследуемый ряд расходится.

2. Исследовать на сходимость .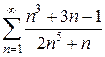

Решение. Сравним данный ряд с рядом 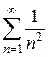. Он сходится.

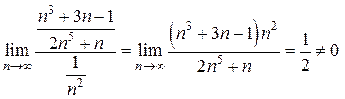. Значит, ряды ведут себя одинаково.

Ответ. Исследуемый ряд сходится.

Замечание. Если общий член ряда имеет вид отношения двух многочленов, то для сравнения подбирается обобщенный гармонический ряд 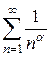, где степень 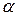находится как разность степеней знаменателя и числителя дроби.

Признак Даламбера. Если для ряда 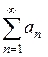с неотрицательными членами существует конечный предел 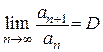, то при 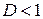ряд сходится, при 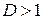ряд расходится.

Пример. Исследовать на сходимость .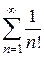

Решение. Для этого ряда .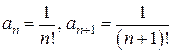

.

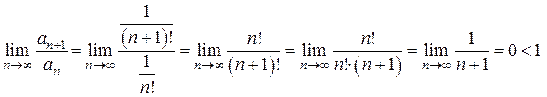Ответ. Исследуемый ряд сходится.

Радикальный признак Коши. Если для ряда 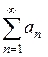с неотрицательными членами существует конечный предел 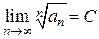, то при 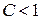ряд сходится, при 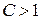ряд расходится.

Пример. Исследовать на сходимость .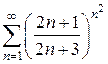

Решение. Для этого ряда .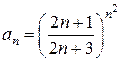

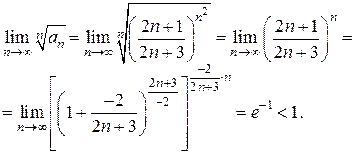
Ответ. Исследуемый ряд сходится.