Сходимость знакочередующихся рядов

Ряды вида 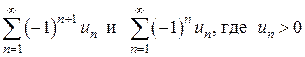называются знакочередующимися рядами.

Замечание. .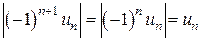

Теорема Лейбница. Если члены знакочередующегося ряда 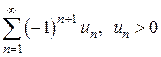удовлетворяют условиям:

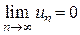и,

начиная с некоторого номера 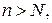все ,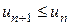

то данный ряд сходится, и абсолютная величина его суммы не превосходит модуля первого члена ряда, т.е. .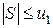

Пример. Исследовать на сходимость .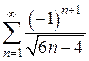

Решение.

; ; .

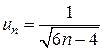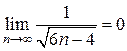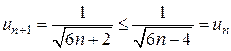Значит, ряд сходится.