Сходимость знакопеременных рядов

Перейдём к рассмотрению рядов, содержащих как положительные, так и отрицательные члены. Такие ряды называют знакопеременными.

Например,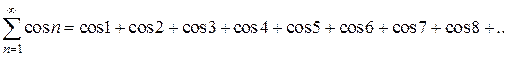

У этого ряда первое слагаемое положительное, следующие три отрицательные, затем снова три положительных и так далее.

Пусть дан ряд 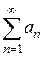, члены которого – числа произвольного знака. Если ряд 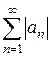сходится, то исходный ряд называют абсолютно сходящимся.

Если же ряд 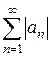расходится, а ряд 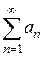сходится, то исходный ряд называют условно сходящимся.

Теорема. Если ряд 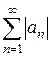сходится, то ряд 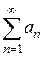сходится (абсолютно).

Пример. Исследовать на сходимость .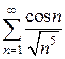

Решение. Рассмотрим ряд из модулей .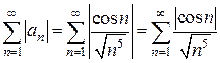

При всех значениях 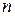верно неравенство .

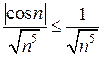Ряд 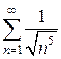сходится, т.к. он является обобщенным гармоническим и степень .

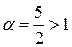Применяя признак сравнения, делаем вывод, что ряд из модулей сходится. Согласно теореме исследуемый ряд также сходится, причем абсолютно.

Ответ. Исследуемый ряд сходится абсолютно.