Теорема 1. Если сходится ряд
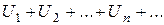 ,
,
то сходится и ряд
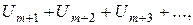
получаемый из данного ряда отбрасыванием первых 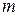 членов (этот последний ряд называют
членов (этот последний ряд называют 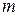 - м остатком исходного ряда); наоборот, из сходимости
- м остатком исходного ряда); наоборот, из сходимости 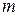 - го остатка ряда вытекает сходимость данного ряда.
- го остатка ряда вытекает сходимость данного ряда.
Теорема. Если сходится ряд
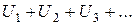
и суммой его является число S, то сходится и ряд
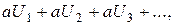
причем сумма последнего ряда равна аS.
Теорема. Если сходится ряды
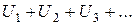 ,
, 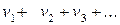 ,
,
имеющие соответственно суммы S и 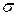 , то сходится и ряд
, то сходится и ряд
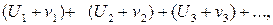
причем сумма последнего ряда равна S +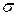 .
.
Теорема. Если ряд
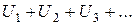
сходится, то 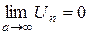 , т.е. при
, т.е. при 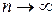 придел общего члена сходящегося ряда равен нулю (необходимый признак сходимости ряда).
придел общего члена сходящегося ряда равен нулю (необходимый признак сходимости ряда).
Таким образом, если 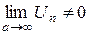 , то ряд расходится.
, то ряд расходится.
Важнейшие признаки сходимости и расходимости рядов с положительными членами.
Первый признак сравнения. Пусть даны два ряда
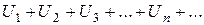 (1)
(1)
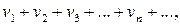 (2)
(2)
причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. 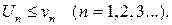 Тогда если сходится ряд (2), то сходится и ряд (1). Если расходится ряд (1), то расходится и ряд (2).
Тогда если сходится ряд (2), то сходится и ряд (1). Если расходится ряд (1), то расходится и ряд (2).
Этот признак остается в силе, если неравенства 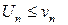 выполняются не при всех п, а лишь начиная с некоторого номера п = N.
выполняются не при всех п, а лишь начиная с некоторого номера п = N.
Второй признак сравнения. Если существует конечный и отличный от нуля предел 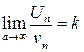 , то оба ряда
, то оба ряда 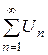 ,
, 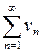 одновременно сходятся или одновременно расходятся.
одновременно сходятся или одновременно расходятся.
Признак Коши. Если для ряда
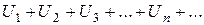
существует 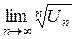 = q, то этот ряд сходится при q <1 и расходится при q >1.
= q, то этот ряд сходится при q <1 и расходится при q >1.
Признак Даламбера. Если для ряда
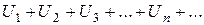
существует 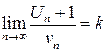 , то этот ряд сходится при k <1 и расходится при k >1.
, то этот ряд сходится при k <1 и расходится при k >1.
Интегральный признак. Если f(x) при 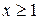 - непрерывная, положительная и монотонная убывающая функция, то ряд
- непрерывная, положительная и монотонная убывающая функция, то ряд 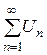 , где
, где 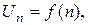 сходится или расходится в зависимости от того, сходится или расходится интеграл
сходится или расходится в зависимости от того, сходится или расходится интеграл
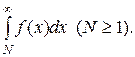
Знакочередующимся рядом называется ряд вида
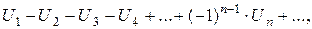
где 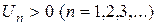 .
.
Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, а общий член стремится к нулю, т.е. если выполняется следующие два условия: 1) 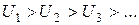 и
и 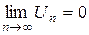 .
.
Возьмем п -ю частичную сумму сходящегося знакочередующегося ряда, для которого выполняется признак Лейбница
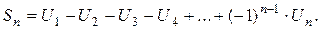
пусть 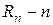 -й остаток ряда. Его можно записать как разность между суммой ряда S и п -й частичной суммой
-й остаток ряда. Его можно записать как разность между суммой ряда S и п -й частичной суммой 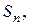 т.е.
т.е. 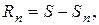
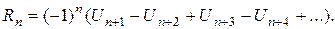
Величина 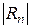 оценивается с помощью неравенства
оценивается с помощью неравенства 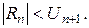
Знакопеременный ряд
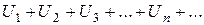
сходится, если сходится ряд
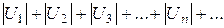
В этом случае исходный ряд 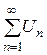 называется абсолютно сходящимся. Сходящийся ряд
называется абсолютно сходящимся. Сходящийся ряд 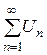 называется условно сходящимся, если ряд
называется условно сходящимся, если ряд 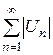 расходится.
расходится.
Пример. Исследовать сходимость ряда
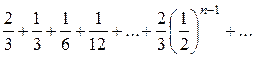
Решение: Данный ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем его сумму 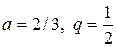 (знаменатель геометрической прогрессии). Следовательно
(знаменатель геометрической прогрессии). Следовательно
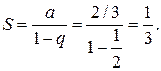
Пример. Исследовать сходимость ряда 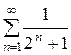 .
.
Решение: Член данного ряда меньше соответствующих членов ряда 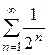 , т.е. ряда
, т.е. ряда 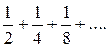
Но последний ряд сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, сходится и данный ряд.
Пример. Исследовать сходимость ряда
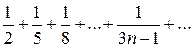
Решение: Сравним ряд с гармоническим рядом, у которого 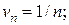
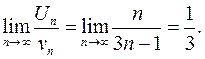
Следовательно, данный ряд расходится.
Пример. Исследовать сходимость ряда
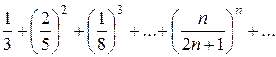
Решение: Здесь удобно применить признак Коши, поскольку 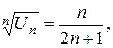 а предел
а предел
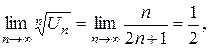
т.к. 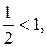 то ряд сходится.
то ряд сходится.
Пример. Исследовать сходимость ряда
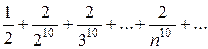 .
.
Решение: Применим признак Даламбера: имеем
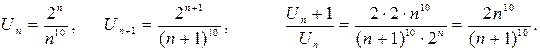
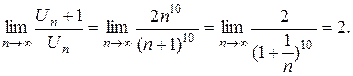
Т.к. 2 > 1, то ряд расходится.
Пример. Исследовать сходимость ряда
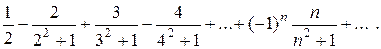
Решение: Применим признак Лейбница. Так как
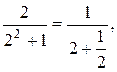
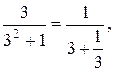
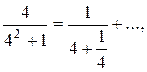
то 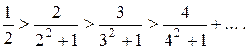
Следовательно, выполнено первое условие признака Лейбница. Так как
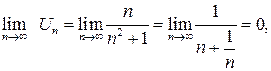
то выполняется и второе условие. Значит, данный ряд сходится.
Пример. Исследовать сходимость ряда
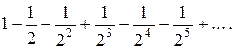
Решение: Составим ряд из абсолютных величин
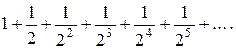
Этот ряд бесконечно убывающая геометрическая прогрессия п, следовательно, данный ряд сходится, причем абсолютно.
Функциональные ряды
Ряд 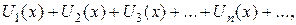
члены которого – функции от х, называются функциональным. Совокупность значений х, при которых функции 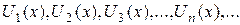 определены и ряд
определены и ряд 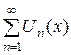 сходится, называют областями сходимости функционального ряда. Каждому значению из области сходимости Х соответствует определенное значение величины
сходится, называют областями сходимости функционального ряда. Каждому значению из области сходимости Х соответствует определенное значение величины 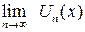 .Эту величину называют суммой функционального ряда и обозначают через S(x).
.Эту величину называют суммой функционального ряда и обозначают через S(x).
Функциональный ряд вида 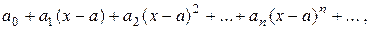
где 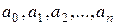 - действительные числа, называется степенным.
- действительные числа, называется степенным.
Основное свойство степенных рядов состоит в том, что если степенной ряд сходится при 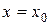 , то он сходится (и притом абсолютно) при всяком значении х, удовлетворяющем неравенству
, то он сходится (и притом абсолютно) при всяком значении х, удовлетворяющем неравенству 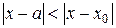 (теорема Абеля).
(теорема Абеля).
Одним из следствий теорем Абеля является факт существования для всякого степенного ряда интервала сходимости 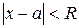 , или
, или 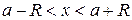 с центром в точке
с центром в точке 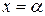 , внутри которого степенной ряд абсолютно сходится и вне которого он расходится. На концах интервала сходимости (в точках
, внутри которого степенной ряд абсолютно сходится и вне которого он расходится. На концах интервала сходимости (в точках 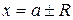 ) различные степенные ряды ведут себя по-разному: одни сходятся абсолютно на обоих концах, другие - либо условно сходятся на обоих концах, либо на одном из них условно сходятся, на другом расходятся, третьи – расходятся на обоих концах.
) различные степенные ряды ведут себя по-разному: одни сходятся абсолютно на обоих концах, другие - либо условно сходятся на обоих концах, либо на одном из них условно сходятся, на другом расходятся, третьи – расходятся на обоих концах.
Число R называется радиусом сходимости степенного ряда. В частных случаях радиус сходимости ряда R может быть равен нулю или бесконечности. Если R=0, то степенной ряд сходится лишь при х = а; если же R = 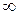 , то ряд сходится на всей числовой оси.
, то ряд сходится на всей числовой оси.
Для отыскания интервала и радиуса сходимости степенного ряда можно пользоваться одним из следующих способов.
1 способ. Если среди коэффициентов ряда 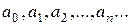 нет равных нулю, т.е. ряд содержит все целые положительные степени разности х-а, то
нет равных нулю, т.е. ряд содержит все целые положительные степени разности х-а, то
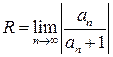 (3)
(3)
при условии, что этот предел (конечный или бесконечный) существует.
2 способ. Если исходный ряд имеет вид
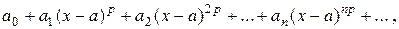
(где р- целое положительное число: 2,3,…), то
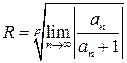 (4)
(4)
3 способ. Если среди коэффициентов ряда есть равные нулю и последовательность оставшихся в ряде показателей степенной разности 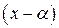 любая, то
любая, то
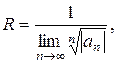 (5)
(5)
где 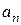 - коэффициенты, отличные от нуля.
- коэффициенты, отличные от нуля.
4. способ. Во всех случаях интервал сходимости ряда можно находить, применяя непосредственно признак Даламбера или признак Коши ряду, составленному из абсолютных величин членов исходного ряда.
Степенные ряды обладают следующим свойством: ряды, полученные почленным дифференцированием и интегрированием степенного ряда, имеют тот же интервал сходимости и их сумма внутри интервала сходимости равны соответственно производной и интегралу от суммы первоначального ряда. Если
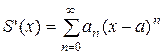 , то
, то
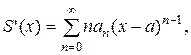
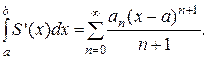
где – R<x-a<R.
Операцию почленного дифференцирования и интегрирования можно произвести над степенным рядом сколько угодно раз.
Пример. Исследовать сходимость ряда
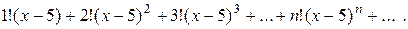
Решение: 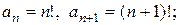 значит
значит 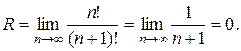
Ряд сходится только при 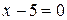 , т.е. в точке х =5.
, т.е. в точке х =5.
Пример. Исследовать сходимость ряда
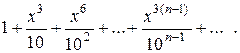
Решение: Ряд является геометрической прогрессией со знаменателем q=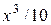 . Он сходится, если
. Он сходится, если 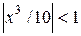 и расходится, если
и расходится, если 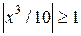 . Следовательно, промежуток сходимости ряда определяется двойным неравенством
. Следовательно, промежуток сходимости ряда определяется двойным неравенством 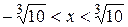 . Там же результат можно получить, используя формулы (4), (5).
. Там же результат можно получить, используя формулы (4), (5).
Пример. Исследовать сходимость ряда
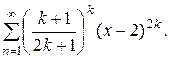
Решение: В данном случае имеем 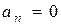 при п=2k-1 и
при п=2k-1 и 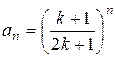 при п=2k. Для отыскания радиуса сходимости удобнее всего использовать формулу (5).
при п=2k. Для отыскания радиуса сходимости удобнее всего использовать формулу (5).
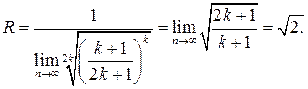
Исследуем ряд на концах интеграла сходимости. Полагая 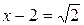 , получаем числовой ряд
, получаем числовой ряд
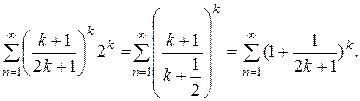
Но 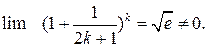 Таким образом, при х -2
Таким образом, при х -2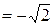 . Итак, область сходимости данного ряда
. Итак, область сходимости данного ряда 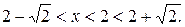
Пример. Исследовать сходимость ряда
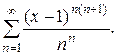
Решение: Применим признак Коши, полагая
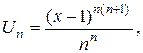
получаем 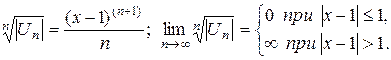
Таким образом, ряд сходится, если 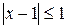 , т.е.
, т.е. 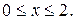
Пример. Исследовать сходимость ряда
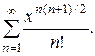
Решение: Применяем признак Даламбера, полагая
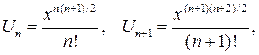
полагаем
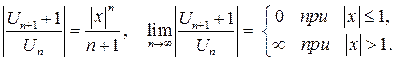
ряд сходится, если 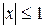 , т.е.
, т.е. 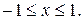
Разложение функций в степенные ряды.
Ряд Тейлора. Ряд Маклорена.
Всякая функция, бесконечно дифференцируемая в интервале 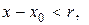 т.е.
т.е. 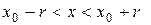 , может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
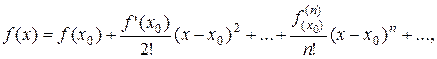
если в этом интервале выполняется условие
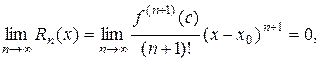
где 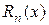 - остаточный член формулы Тейлора (или остаток ряда),
- остаточный член формулы Тейлора (или остаток ряда),
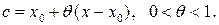
При 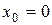 получается степенной ряд Маклорена:
получается степенной ряд Маклорена:
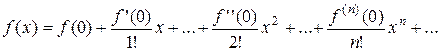
Если в некотором интервале, содержащем точку 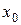 , при любом п выполняется неравенство
, при любом п выполняется неравенство 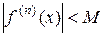 , где М – положительная постоянная, то
, где М – положительная постоянная, то 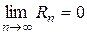 и функция f(x) разложима в ряд Тейлора.
и функция f(x) разложима в ряд Тейлора.
Разложение элементарных функций в ряд Маклорена.
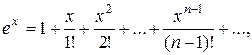
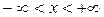 ;
;
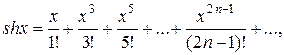
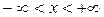 ;
;
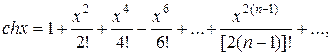
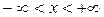 ;
;
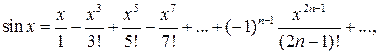
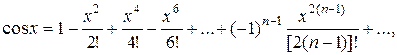
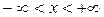
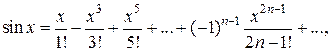
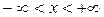
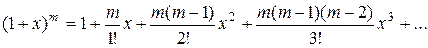
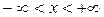
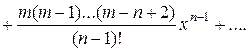
Это последнее разложение имеет место
при 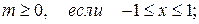
при 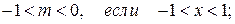
при 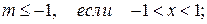
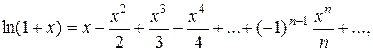
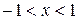 ;
;
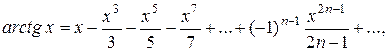
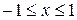 .
.
Пример. Разложить в ряд по степеням х функцию 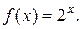
Решение: Найдем значения функции и её производных при х =0.
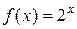 ,
, 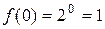 ,
,
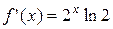 ,
, 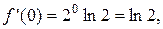
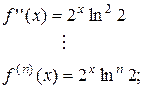 ,
, 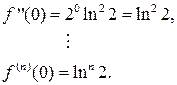
Так как 0 < ln 2<1, то при фиксированном х имеет место неравенство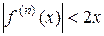 для любого п. Следовательно, функция может быть представлена в виде суммы ряда Маклорена:
для любого п. Следовательно, функция может быть представлена в виде суммы ряда Маклорена:
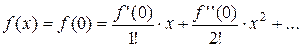 ,
,
поэтому
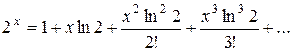
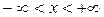
Пример. Разложить в ряд по степеням х функцию 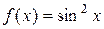
Решение: Продифференцируем функцию п +1 раз:
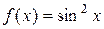 ,
,
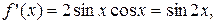
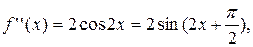
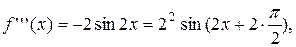
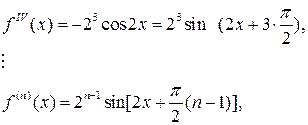
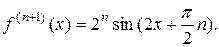
В точке х = 0 находим  , а значение f(n+1) (х) определяем в точке х=с. Получаем f(0)=0,
, а значение f(n+1) (х) определяем в точке х=с. Получаем f(0)=0, 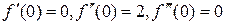 ,
, 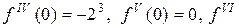
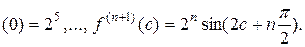
Находим остаточный член:
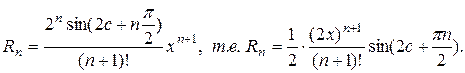
Так как 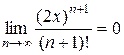 при любом х, а
при любом х, а 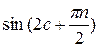 величина ограниченная, то
величина ограниченная, то 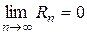 . Следовательно, функцию
. Следовательно, функцию 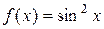 можно представить в виде суммы ряда Маклорена
можно представить в виде суммы ряда Маклорена
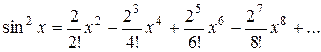 .
.
Пример. Разложить 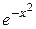 в ряд по степеням х.
в ряд по степеням х.
Решение: B разложении
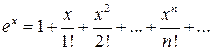
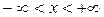 .
.
Заменим х на –х2; получим
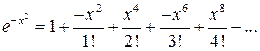
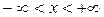 .
.
Пример. Разложить lnx в ряд по степеням х -1
Решение: B разложении
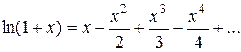
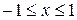 .
.
Заменим х на х - 1; получим
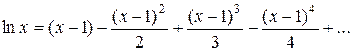
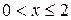 .
.
Пример. Разложить в ряд по степеням х -2 функцию 1/ х.
Решение: Воспользуемся равенством 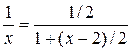 . Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом
. Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом 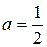 и знаменателем
и знаменателем 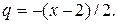
Отсюда получаем
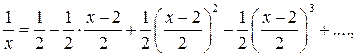
то есть
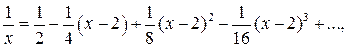
так как 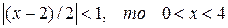 .
.
 2014-01-25
2014-01-25 1706
1706