Разложение данной функции в виде ряда Маклорена можно получить обычным способом, но намного эффективнее это выполнить основываясь на свойствах степенных рядов. А именно, зная, что степенной ряд можно интегрировать на любом отрезке из интервала сходимости ряда, можно получить:
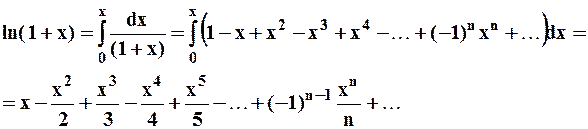 ,
, 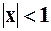 .
.
Область сходимости данного ряда 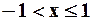 , так как в точке
, так как в точке 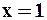 получаем ряд Лейбница, который сходится. В левой же границе получаем гармонический ряд.
получаем ряд Лейбница, который сходится. В левой же границе получаем гармонический ряд.
Аналогично получается разложение функции 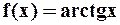 . Рассмотрим ряд:
. Рассмотрим ряд:
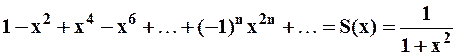
при 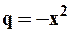 и
и 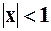 .
.
Тогда: 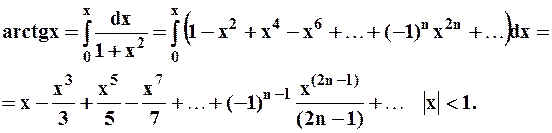
 2014-01-25
2014-01-25 815
815








