2014-01-25
777
Рассмотрим разложение функции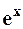 
в ряд Маклорена в окрестности точки 
:
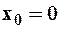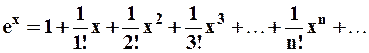. Данное представление можно рассматривать при малых значениях 
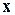и следующим образом: 
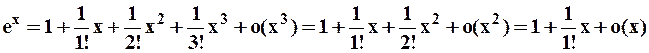и т.д., где обозначено, например, 
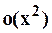–функция, более высокого порядка малости, чем 
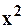при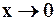 
. В действительности, отношение остатка ряда к 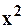будет стремиться к 
:
.
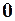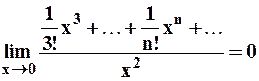Этот факт будем использовать при представлении функции частью ряда, содержащего необходимое число слагаемых. Число удерживаемых слагаемых в ряде определяется величиной малости выражения, стоящего в знаменателе. Рассмотрим на примерах:
Пример 1. Вычислить значение предела:
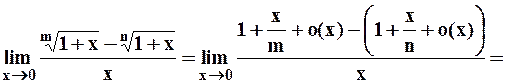
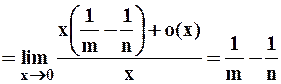. Здесь принято, что 
.
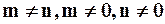Пример 2. Вычислить значение предела:
.
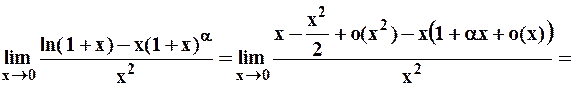
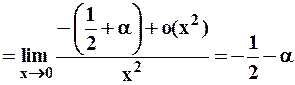Здесь и в дальнейшем используем следующий факт: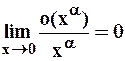 
.
Пример 3. Вычислить значение предела:
