Уравнение неразрывности.
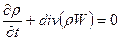 (2.69)
(2.69)
или в частных производных:
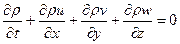
Уравнение Навье-Стокса.
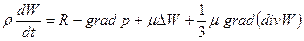 (2.70)
(2.70)
где R — вектор напряжения объемной силы.
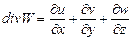 - дивергенции вектора скорости;
- дивергенции вектора скорости; 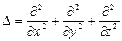 - оператор Лапласа
- оператор Лапласа
В частных производных:
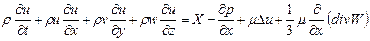
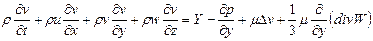
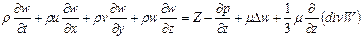
где m - кинематическая вязкость
В вязкой жидкости имеет место прилипание частиц жидкости к стенкам, ограничивающим течение, поэтому при интегрировании дифференциальных уравнений Навье — Стокса нужно использовать в качестве граничного условия равенство нулю скорости течения у стенки (Ww = 0).
В случае несжимаемой жидкости (r = const, div W = 0) уравнения Навье — Стокса прини-мают более простой вид:
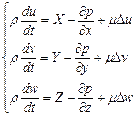 (2.71)
(2.71)
или
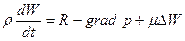
Решение уравнений Навье — Стокса даже для несжимаемой жидкости представляет собой очень сложную задачу. До сих пор удалось решить эти уравнения точно лишь в некоторых простейших случаях, например для течения вязкой жидкости по прямой трубе; для течения между двумя параллельными плоскими стенками, из которых одна неподвижна, а другая движется и др.
Задачи газодинамики вязкой жидкости решаются обычно приближенно путем отбрасывания некоторых членов в уравнениях Навье — Стокса, которые в тех или иных конкретных условиях могут быть малы по сравнению с другими членами.
Уравнение энергии
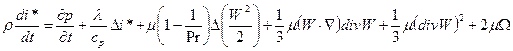 (2.72),
(2.72),
где 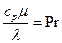 - число Прандтля
- число Прандтля
 2014-01-25
2014-01-25 748
748








