Классическое определение вероятности.
В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных
Каждый из возможных результатов испытания назовём элементарным исходом (элементарным событием).
Те элементарные исходы, которые интересуют нас, называются благоприятными событиями.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов (m) к общему числу всех равновозможных несовместных элементарных исходов (n), образующих полную группу.
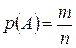
Свойство 1. Вероятность достоверного события равна единице.
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключённое между нулём и единицей.
Классическое определение вероятности можно применять лишь в тех случаях, когда число элементарных исходов конечно и элементарные исходы равновероятны.
Задача.
Решение:
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь m деталей из N деталей, то есть 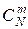 - числу сочетаний из N элементов по m.
- числу сочетаний из N элементов по m.
Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди m деталей ровно k стандартных): k стандартных деталей можно взять из n стандартных деталей 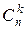 способами; при этом остальные m - k деталей должны быть нестандартными; взять же m - k нестандартных деталей из N - n нестандартных деталей можно
способами; при этом остальные m - k деталей должны быть нестандартными; взять же m - k нестандартных деталей из N - n нестандартных деталей можно 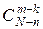 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 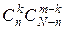
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
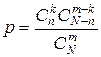
 2014-01-25
2014-01-25 1180
1180