ПОНЯТИЕ. КЛАССИФИКАЦИЯ СОБЫТИЙ.
СЛУЧАЙНЫЕ СОБЫТИЯ.
Лекция 20
Тема: Теория вероятностей.
Время: 2 ч.
Вопросы:
1. Основы теории вероятности.
2. Случайные события. Понятие. Классификация событий.
3. Операции над событиями.
4. Действия над случайными событиями.
5. Эмпирическая вероятность.
6. Классическое определение вероятности.
7. Сведения из комбинаторики.
1. Основы теории вероятностей.
Мы переходим к изучению совершенно новых математических объектов, связанных с понятием случайности. Случайность как явление реальной жизни хорошо нам знакома.
Например: Случайными бывают попутчики, встречи, звонки и т.д. Многое в нашей жизни случайно, т.е. не обусловлено четкими причинно-следственными связями.
Даже в бытовом уровне мы различаем два вида событий – детерминированные и случайные. В детерминированном событии мы точно знаем, что данная причина приведет к единственному и вполне определенному следствию. Мы нажимаем на кнопку, и лампа загорается: между действием и результатом существует четкая однозначная связь. Исход случайного события непредсказуем, он зависит от случайных факторов. Например, подбрасывание монеты или кубика. Нельзя узнать заранее, на какую сторону упадет монета, или какая грань выпадет на кубике.
Существуют также бытовые представления о вероятности. Например, оценивая шансы на выигрыш, мы неосознанно подсчитываем его вероятность.
Теория вероятностей зародилась как наука в XVII в. под влиянием интереса к такому несерьезному занятию, как азартные игры. Дальнейшее развитие теории вероятностей в XVIII в. Связано с именами таких математиков, как Якоб Бернулли (1654 - 1705), Даниил Бернулли (1700 - 1782), Абрахам Де Муавр (1667 - 1754) и Жорж Луи Бюффон (1707 - 1788). Значительный вклад в теорию вероятностей внесли русские математики П.Л.Чебышев (1821 - 1894) и его ученики А.М. Ляпунов (1857 - 1918), А.А.Марков (1856 - 1922).
Мы уже дали некоторую начальную классификацию, разделив, события на детерминированные и случайные. Рассмотрим основные черты случайного события как математического объекта. Какие наблюдения можно сделать, например, при бросании монеты? Во-первых, исход этого эксперимента непредсказуем. Однако возможных исходов всего два: может выпасть либо «орел», либо «решка». Условия реального эксперимента при повторении неизбежно меняются (бросание монеты происходит всегда по-разному). При математическом определении случайного события мы считаем, что эксперимент можно повторить неограниченное число раз при одинаковых условиях. Это важные характеристики случайного события.
События, с неясным исходом, но и не случайные называют неопределенными.
Давайте, при бросании монеты будем наблюдать, за количеством выпадения «орлов». 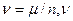 - относительная частота, n – количество испытаний,
- относительная частота, n – количество испытаний, 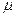 - частота данного случайного события. При увеличении числа испытаний относительная частота события имеет тенденцию к стабилизации. Такое поведение характерно для любого случайного событий и носит название статистической устойчивости.
- частота данного случайного события. При увеличении числа испытаний относительная частота события имеет тенденцию к стабилизации. Такое поведение характерно для любого случайного событий и носит название статистической устойчивости.
Итак, случайное событие характеризуется тремя особенностями:
· Неопределенностью исхода единичного эксперимента;
· Возможностью неограниченного повторения в одинаковых условиях;
· Стабилизацией относительной частоты.
Случайные события в теории вероятностей обычно обозначают прописными латинскими буквами А,В,С и т.д.
Суммой событий А и В (обозначается А+В) называют событие, состоящее в появлении хотя бы одного из двух событий А или В.
Аналогично определяется сумма большего числа событий
Пример 1: Появление чётной грани игральной кости есть сумма трёх событий: выпадение 2, выпадение 4, выпадение 6.
Произведением событий А и В (обозначается А·В) называют событие, состоящее в появлении обоих событий А и В.
Пример 2: Пусть событие А – при бросании двух монет появление герба на первой монете, событие В – появление герба на второй монете; тогда произведение А·В – это появление гербов на обеих монетах.
Произведение несовместных событий – событие невозможное. Сумма и произведение событий аналогичны объединению и пересечению множеств, соответственно.
Вероятность суммы А+В несовместимых событий А и В равна сумме вероятностей событий А и В, т.е. Р(А+В)=Р(А)+Р(В)
 2014-01-25
2014-01-25 851
851








