Говорят, что событие В следует из события А, если событие В происходит всегда, когда произошло событие А.
События А и В равны, если из А следует В и из В следует А.
Суммой двух событий А и В называется событие А+В, состоящее в том, что произошло событие А или событие В.
Сложение событий удовлетворяет коммутативному и ассоциативному законам.
А + В = В + А
А + (В + С) = (А + В) + С
Из события А следует сумма этого события с любым событием В:
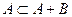
Пример 3: Стрельба по мишени. Пусть стрелок сделал 5 выстрелов по мишени.
Событие С = «стрелок попал не меньше трех раз» есть сумма трех событий:
С=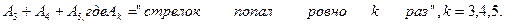
Событие D = «стрелок попал хотя бы один раз» произойдет, если стрелок попал один раз, или два раза, или три раза и т.д. Значит, D=A1+A2+A3+A4+A5.
Произведением двух событий А и В называется событие АВ, состоящее в том, что событие А и событие В произошли одновременно. Умножение событий так же, как и сложение, коммутативно и ассоциативно.
А* В = В * А,
А*(В * С)=(А * В)*С
Из события АВ следуют событие А и событие В:
АВ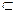 А, АВ
А, АВ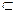 В
В
Сложение и умножение событий удовлетворяют двум дистрибутивным законам.
А*(В + С) = А*В + А*С,
А + В*С = (А+В)*(А+С).
Пример 4: Одновременное бросание двух кубиков. Событие С состоит в том, что сумма чисел на обоих кубиках четна. Это может произойти, когда оба числа четные или оба нечетные. Пусть А1 = «на первом кубике четное число», В1= «на первом кубике нечетное число», А2, В2 – те же события для второго кубика. Тогда С = А1А2+В1В2.
Событие 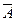 называется противоположным событию А, если оно состоит в том, что не произошло событие А. Например, выпадение «орла» при бросании монеты противоположно выпадению «решки».
называется противоположным событию А, если оно состоит в том, что не произошло событие А. Например, выпадение «орла» при бросании монеты противоположно выпадению «решки».
Событие называется достоверным, если оно происходит всегда. Например, событие состоящее в том, что при бросании монеты выпадает «орел» или «решка», является достоверным.
Событие, не наступающее никогда, называется невозможным. Например, одновременное выпадение «орла» и «решки» невозможно.
События образуют полный набор, если они несовместны, а их сумма есть достоверное событие. Например, при бросании монеты полный набор состоит из двух событий: выпадение «орла» или «решки». Действительно, событие «выпал орел или решка» является достоверным.
 2014-01-25
2014-01-25 1267
1267








