КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Будем предполагать, что данный эксперимент имеет N возможных исходов, все они равновозможные и несовместны, т.е. никакие два из них не могут наступить одновременно.
Вероятностью Р(А) события А называется отношение числа благоприятных исходов m(А) к общему числу N несовместных равновозможных исходов:
Р(А)=m(A)\N – классическое определение вероятности.
Выполняются три свойства:
- Для любого случайного события А 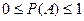 .
.
- Пусть события А и В несовместны. Тогда Р(А+В)=Р(А)+Р(В).
- Пусть события 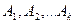 образуют полный набор. Тогда
образуют полный набор. Тогда 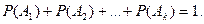
Пример 5: Рассмотрим эксперимент с бросанием монеты. У него два несовместных и равновозможных исхода: «орел» и «решка». Значит вероятность появления «орла» равна ½, вероятность появления решки равна также ½.
Пример 6: Пусть в урне находятся 2 белых и 2 чёрных шара, событие А – вынут белый шар, событие В – вынут чёрный шар. Тогда, Р(А) = 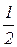 ; Р(В) =
; Р(В) = 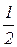 . События А и В независимые, если после первого испытания шар кладётся в урну и шары перемешиваются. Если вынутый шар в первом испытании не кладётся обратно в урну, то вероятность вынуть во втором испытании шар другого цвета возрастает с
. События А и В независимые, если после первого испытания шар кладётся в урну и шары перемешиваются. Если вынутый шар в первом испытании не кладётся обратно в урну, то вероятность вынуть во втором испытании шар другого цвета возрастает с 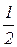 до
до 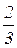 . Таким образом, события А и В оказываются зависимыми.
. Таким образом, события А и В оказываются зависимыми.
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое событие уже наступило, т.е. Р(А·В) = Р(А)·РА(В)
Доказательство: Пусть событию А благоприятствуют m, а событию А·В – k равновозможных элементарных исходов из общего их количест ва n (Рис. 32). Тогда Р(А) =
ва n (Рис. 32). Тогда Р(А) = 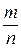 ; P(А·B) =
; P(А·B) = 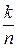 . С другой стороны, если событие А произошло, то возможны лишь те m элементарных исходов, которые благоприятствовали событию А, причём k из них благоприятствовали событию В тоже. Значит РА(В) =
. С другой стороны, если событие А произошло, то возможны лишь те m элементарных исходов, которые благоприятствовали событию А, причём k из них благоприятствовали событию В тоже. Значит РА(В) = 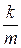 . Следовательно,
. Следовательно,
P(А·B)= 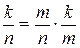 =Р(А) ·РА(В)
=Р(А) ·РА(В)
Поскольку АВ = ВА имеем: Р(А·В)=Р(В·А)=Р(В)·РВ(А)
Следствие: Для любых событий А и В справедливо равенство
Р(А)·РА(В) = Р(В)·РВ(А)
Доказательство: Действительно, если А и В независимые события, то РА(В) = Р(В). С другой стороны, Р(А·В) = Р(А)·РА(В). Тогда Р(А·В) = Р(А)·Р(В).
Th: Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их произведения
Р(А+В)=Р(А) + Р(В) - Р(А·В)
Доказательство:
 Пусть из вcего числа n элементарных событий k благоприятствуют событию А, l – событию В, m – событиям А и В одновременно (Рис. 33). Значит событию А+В благоприятствуют k+l-m элементарных событий.
Пусть из вcего числа n элементарных событий k благоприятствуют событию А, l – событию В, m – событиям А и В одновременно (Рис. 33). Значит событию А+В благоприятствуют k+l-m элементарных событий.
Тогда, 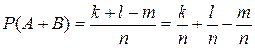 = Р(А) + Р(В) – Р(А·В)
= Р(А) + Р(В) – Р(А·В)
Задача: Два стрелка стреляют в одну и ту же цель, причём вероятность поражения цели первым стрелком 0,8, а вторым стрелком 0, 5. Оба стрелка стреляют одновременно и один раз. Какова вероятность того, что цель будет поражена хотя бы одним из стрелков?
Решение: Пусть А – попадание в цель первым стрелком, В – вторым стрелком, А+В – поражение цели хотя бы одним стрелком, А·В – поражение цели обоими стрелками. Тогда Р(А+В)=0,8 + 0,5 – Р(А·В). Считая события А и В независимыми имеем: Р(А·В) = Р(А)·Р(В) = 0,8·0,5 = 0,4
Ответ: Р(А+В) = 0,9
Задача: В ящике имеются 7 белых и 5 чёрных шаров, отличающихся лишь цветом. Опыт состоит в том, что сначала вынимают (не глядя) один шар и, не опуская его обратно, вынимают ещё один шар. Какова вероятность, что оба вынутых шара чёрные?
Решение: Появление первого чёрного шара (событие А) имеет вероятность 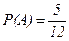 . Если первый шар оказался чёрным, то условная вероятность события В – появление второго чёрного шара (при условии, что первый шар был чёрным) – равна РА(В)=
. Если первый шар оказался чёрным, то условная вероятность события В – появление второго чёрного шара (при условии, что первый шар был чёрным) – равна РА(В)=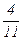 , т.к. перед выниманием второго шара осталось 11 шаров, из них 4 чёрных. Вероятность вынуть два чёрных шара подряд можно подсчитать по формуле:
, т.к. перед выниманием второго шара осталось 11 шаров, из них 4 чёрных. Вероятность вынуть два чёрных шара подряд можно подсчитать по формуле:
P(А·B) = Р(А) ·РА(В) 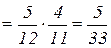
Th. (формула полной вероятности) Вероятность события А, которое может наступить лишь при условии появления одного из n попарно несовместимых событий В1, В2, В3, …, B n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А, т.е.
Р(А)=Р(В1)·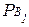 (А) + Р(В2)·
(А) + Р(В2)·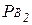 (А) + … + Р(Вn)·
(А) + … + Р(Вn)·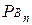 (A)
(A)
Доказательство: Событие А может наступить лишь при условии наступления одного из событий В1, В2, В3, …, Bn, т.е. В1А + В2А + В3А + … + BnА, причём события В1А, В2А, В3А, …, BnА несовместимы, т.к. несовместимы события В1, В2, В3, …, Bn. Тогда на основании теорем сложения и умножения вероятностей имеем Р(А)=Р(В1А) + Р(В2А) + Р(В3А) + … + Р(BnА) = Р(В1)·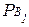 (А) + +Р(В2)·
(А) + +Р(В2)·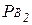 (А) + … + Р(Вn)·
(А) + … + Р(Вn)·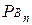 (A) или
(A) или 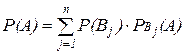
При условиях формулы полной вероятности справедлива формула Байеса:
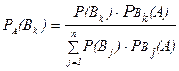 , где k=1, 2, …, n
, где k=1, 2, …, n
Задача: Для приёма зачёта преподаватель заготовил 50 задач: 20 задач по дифференциальному исчислению, 30 – по интегральному исчислению. Для получения зачёта студент должен решить первую же достающуюся наугад задачу. Какова вероятность для студента сдать зачёт, если он умеет решать 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению.
Решение: Вероятность получить задачу по дифференциальному исчислению (событие В1) равна Р(В1)=0,4, по интегральному исчислению (событие В2) – Р(В2)=0,6. Если событие А означает, что задача решена, то 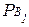 (А)=0,9,
(А)=0,9, 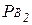 (А)=0,5. Тогда Р(А)=0,4·0,9 + 0,6·0,5 = 0,36 + 0,3 = 0,66
(А)=0,5. Тогда Р(А)=0,4·0,9 + 0,6·0,5 = 0,36 + 0,3 = 0,66
Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного конечного множества и размещения их в каком-либо порядке.
Чтобы пользоваться классическим определением вероятности нужно уметь подсчитывать общее число исходов эксперимента и число благоприятных исходов. Такой подсчет сводится к перебору вариантов. Раздел математики, в котором исследуются различные задачи на перебор, называется комбинаторикой.
Рассмотрим некоторые задачи на перебор.
Пусть имеется n различных элементов.
Перестановкой из n различных элементов х1, х2, …, хn называют каждую последовательность этих элементов в каком-либо порядке.
Перестановки ( от слова переставить ) отличаются друг от друга только порядком следования элементов. Например, 3, 1, 4, 2 и 4, 3, 1, 2 – две различные перестановки цифр 1, 2, 3, 4.
Число Pn всех перестановок данных n элементов равно произведению всех натуральных чисел от 1 до n, т.е. Pn=1·2·3·…·n. Такое произведение обозначают n! (читают “ n факториал”). Полагают, что 0!=1!=1. Например, 6 волейболистов можно разместить на площадке 6!=1·2·3·4·5·6=720 способами. Справедлива формула: (n+1)!=n!(n+1)
Некоторые значения факториала:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| n! | 1 | 2 | 6 | 24 | 120 | 720 | 5040 | 40320 | 362880 | 3628800 |
Последовательность, составленную в каком-либо определённом порядке из n возможных элементов по m (m ≤ n) выбранных, где ни один элемент не повторяется дважды называют размещением из n по m.
Задача о рассаживании. Из группы в n человек требуется рассадить за столом m человек (m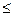 n). Сколькими способами это можно сделать?
n). Сколькими способами это можно сделать?
Пронумеруем m стульев. Тогда на первый стул можно усадить одного из n человек. Пусть первое место уже занято. Тогда на второе остается n-1 претендент. Каждая из n возможностей занять первое место сочетается с n-1 возможностью для второго. Т.о., существует n(n-1) вариантов рассаживания на первые два стула. Последний m-й стул может занять соответственно n-(m-1)=n-m+1 человек, всего получается n(n-1)(n-2)… (n-m+1) вариантов рассаживания. Искомое число вариантов рассаживания называется числом размещения из n по m и обозначается 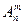 :
:
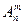 = n(n-1)(n-2)… (n-m+1), если n=m, то
= n(n-1)(n-2)… (n-m+1), если n=m, то 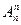 =n(n-1)(n-2)…2*1
=n(n-1)(n-2)…2*1
Произведение n первых натуральных чисел называется «n-факториал» и обозначается n!. 0!=1.
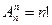
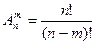 .
.
Пример: 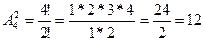 , четырех человек можно рассадить по двое 12 способами.
, четырех человек можно рассадить по двое 12 способами.
Пример 7: Выбор 4 человек из числа 9 предложенных является размещением из 9 по 4. Таких размещений 3024.
Число размещений из n по m обозначается 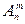 (читается «А из n по m»). Справедлива формула:
(читается «А из n по m»). Справедлива формула:
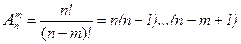
Пример 8: Число размещений из 9 по 4 равно 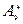 =9·8·7·6=3024
=9·8·7·6=3024
Последовательность, составленную в произвольном порядке из n возможных элементов по m (m ≤ n) выбранных, где ни один элемент не повторяется дважды называют сочетанием из n по m.
Различные сочетания отличаются друг от друга только самими входящими в них элементами. Например, 1, 2, 3 и 2, 1, 3 составляют разные размещения, но одно и то же сочетание из четырёх по три, если исходная последовательность имеет вид: 1, 2, 3, 4.
Число сочетаний из n по m обозначается 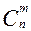 (читается “С из n по m”).
(читается “С из n по m”).
Задача о выборе. Сколькими способами можно выбрать m человек из группы в n человек (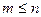 )?
)?
Справедлива формула: 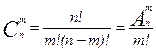
Пример 9: Число сочетаний из 15 по 11 равно
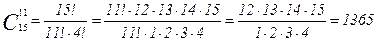
 2014-01-25
2014-01-25 719
719








