План лекции
Лекция 4. Числовые ряды
4.1. Введение
4.2. Числовые ряды
4.3. Знакопеременные ряды
Под рядом понимается бесконечная сумма. Простейшие случаи вычисления рядов с конечным числом слагаемых встречаются в египетских папирусах и вавилонских клинописях II тысячелетия до н. э. Средние века можно считать временем зарождения теории рядов. Например, в 1350 г. Н. Орем доказал расходимость гармонического ряда. Большой вклад в эту теорию внесли Ньютон, Эйлер, Лейбниц, Тейлор, Даламбер, Коши, Абель, Дирихле и другие математики. До XIX века ряды были средством вычисления и интегрирования функций, методом приближённого решения дифференциальных уравнений. Затем они стали самостоятельным объектом изучения.
Ряды являются необычным объектом, поскольку они имеют дело с бесконечностью, которую человеческий разум до конца осознать не в состоянии. Действительно, чтобы просуммировать бесконечное число слагаемых нужно жить бесконечно долго.
Немного понять, что такое ряд, можно на таком простом примере. Возьмём отрезок [0, 1] на числовой оси (рис.1).
|
|
|
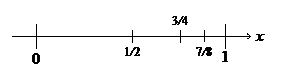
Рис. 1. К вычислению суммы ряда
Разделив его пополам, получим отрезок длиной ½. К этому отрезку прибавим половину оставшейся части длиной ¼. Затем опять разделим оставшийся отрезок пополам и присоединим эту часть 1 / 8 к двум предыдущим. Если этот процесс деления на каком-то шаге остановить, то до конца отрезка [0, 1] мы не дойдём, останется пусть крохотный, но конечный отрезок. До 1 можно дойти только в том случае, если процесс деления (а разделить на 2 можно любое как угодно малое число) и присоединения продолжать до бесконечности (человеческой жизни на это не хватит). Вот это и есть ряд, и мы знаем его сумму:
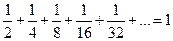 .
.
Здесь троеточие означает, что слагаемых бесконечное количество.
 2014-01-25
2014-01-25 709
709








