Основные понятия
Рассмотрим бесконечную последовательность чисел 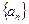 , т.е. множество чисел, в котором каждому натуральному числу n по определённому правилу соответствует некоторое число an. Выражение вида
, т.е. множество чисел, в котором каждому натуральному числу n по определённому правилу соответствует некоторое число an. Выражение вида 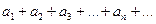 называется числовым рядом, сами числа – членами ряда,
называется числовым рядом, сами числа – членами ряда, 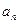 – общим членом ряда. Коротко ряд записывают так:
– общим членом ряда. Коротко ряд записывают так: 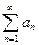 .
.
Суммы 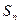 , в которых присутствуют только n первых членов ряда, называются частичными суммами ряда.
, в которых присутствуют только n первых членов ряда, называются частичными суммами ряда.
Числовой ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел 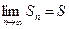 . Число S называется суммой ряда.
. Число S называется суммой ряда.
Если предел 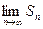 не существует, то ряд называется расходящимся.
не существует, то ряд называется расходящимся.
Пример 1. Дана бесконечная геометрическая прогрессия 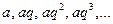 . Составим ряд
. Составим ряд
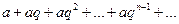 (1)
(1)
и исследуем его на сходимость, исходя из определения сходимости ряда. Для этого составим частичную сумму 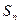 =
=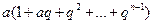 . Из школьного курса математики известно, что
. Из школьного курса математики известно, что 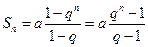 . Напомним, как это получается. Для доказательства произведём деление
. Напомним, как это получается. Для доказательства произведём деление
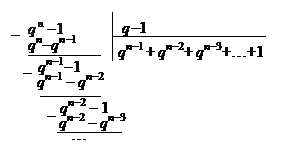
Вычислим теперь предел 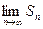 , учитывая, что здесь возможны три случая:
, учитывая, что здесь возможны три случая:
1) 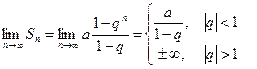 , (2)
, (2)
2) если q = 1, то 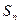 =
=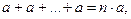 и
и 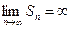 ,
,
3) если q = –1, то 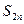 =
=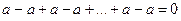 , и
, и 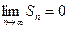 , а
, а 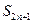 =
= 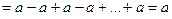 , и
, и 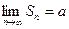 . Значит, последовательность частичных сумм единого предела не имеет.
. Значит, последовательность частичных сумм единого предела не имеет.
Поэтому делаем вывод: геометрическая прогрессия сходится, если 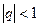 и расходится при
и расходится при 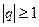 .
.
Пример 2. Доказать расходимостьряда
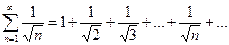 .
.
Решение. Оценим частичную сумму ряда:
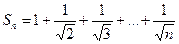 >
> 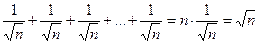 , т.е.
, т.е. 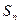 >
> 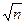 ,
,
а предел частичной суммы равен бесконечности (по известной теореме о пределах: если xn > yn, то 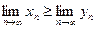 ):
): 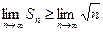 = ¥. Значит, данный ряд расходится.
= ¥. Значит, данный ряд расходится.
Свойства сходящихся рядов
Рассмотрим два ряда 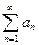 и
и 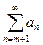 . Второй ряд получен из первого путём отбрасывания первых m его членов. Этот ряд называется остатком ряда и обозначается rn.
. Второй ряд получен из первого путём отбрасывания первых m его членов. Этот ряд называется остатком ряда и обозначается rn.
Теорема 1. Если члены сходящегося ряда умножить на некоторое число С, то сходимость ряда не нарушится, а сумма умножится на С.
Теорема 2. Два сходящихся ряда можно почленно складывать (вычитать) и сумма полученного ряда будет равна 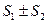 , где
, где 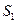 - сумма первого ряда, а
- сумма первого ряда, а 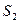 – сумма второго.
– сумма второго.
Теорема 3. Если сходится ряд, то сходится любой из его остатков. Из сходимости остатка ряда следует сходимость самого ряда.
Можно сказать и по-другому: на сходимость ряда не влияет отбрасывание (или приписывание) конечного число членов ряда. И это свойство самое замечательное. Действительно, пусть сумма ряда равна бесконечности (ряд расходится). Мы складываем очень большое, но конечное число членов ряда. Эта сумма может быть очень большим, но, опять же, конечным числом. Так, значит, сумма остатка ряда, а там члены ряда уже ничтожно малые числа, всё равно равна бесконечности за счёт бесконечности числа слагаемых.
Теорема 4. Необходимый признак сходимости.
Если ряд сходится, то его общий член an стремится к нулю, т.е. 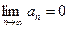 .
.
Доказательство. Действительно,
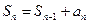 ,
, 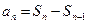 , и если ряд сходится, то
, и если ряд сходится, то 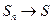 и
и 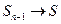 , а значит,
, а значит, 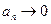 при
при 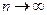 .
.
Отметим, что этот признак не является достаточным, т.е. ряд может расходиться, а его общий член стремится к нулю. В примере 2 ряд 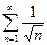 расходится, хотя его общий член
расходится, хотя его общий член 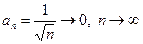 .
.
Но если аn не стремится к нулю при 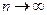 , то ряд является расходящимся (достаточный признак расходимости ряда).
, то ряд является расходящимся (достаточный признак расходимости ряда).
Сходимость рядов с положительными членами
Ряд 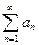 называется положительным, если все
называется положительным, если все 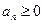 .
.
Частичные суммы такого ряда Sn образуют возрастающую последовательность, так как каждая предыдущая меньше следующей, т.е. 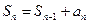 . Из теории пределов известно (теорема Больцано-Вейерштрасса), что если возрастающая последовательность ограничена сверху (т.е. для всех Sn существует такое число М, что Sn < М для всех n), то она имеет предел. Отсюда следует следующая теорема.
. Из теории пределов известно (теорема Больцано-Вейерштрасса), что если возрастающая последовательность ограничена сверху (т.е. для всех Sn существует такое число М, что Sn < М для всех n), то она имеет предел. Отсюда следует следующая теорема.
Теорема. Ряд с положительными членами сходится, если частичные суммы его ограничены сверху, и расходится в противном случае.
На этом свойстве основаны все достаточные признаки сходимости рядов с положительными членами. Рассмотрим основные из них.
Признак сравнения
Рассмотрим два ряда с неотрицательными членами: 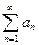 - (3) и
- (3) и 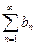 - (4), причём
- (4), причём 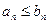 , начиная с некоторого n. Тогда из сходимости ряда (4) следует сходимость ряда (3). А из расходимости ряда (3) следует расходимость ряда (4).
, начиная с некоторого n. Тогда из сходимости ряда (4) следует сходимость ряда (3). А из расходимости ряда (3) следует расходимость ряда (4).
Иначе: если сходится ряд с б?льшими членами, то сходится и ряд с меньшими членами; если расходится ряд с меньшими членами, то расходится и ряд с б?льшими членами.
Пример. Исследовать на сходимость ряд 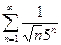 .
.
Решение. Общий член ряда 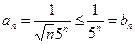 , а ряд
, а ряд 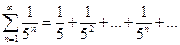 есть бесконечная сумма членов геометрической прогрессии со знаменателем
есть бесконечная сумма членов геометрической прогрессии со знаменателем 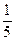 < 1, т.е. это сходящийся ряд. По признаку сравнения (т.к. сходится ряд с б?льшими членами, то сходится и ряд с меньшими) данный ряд
< 1, т.е. это сходящийся ряд. По признаку сравнения (т.к. сходится ряд с б?льшими членами, то сходится и ряд с меньшими) данный ряд 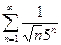 сходится.
сходится.
Признак сравнения в предельной форме
Рассмотрим два ряда 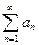 и
и 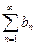 , и пусть
, и пусть 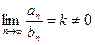 ,
, 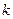 – конечное число. Тогда оба ряда сходятся или расходятся одновременно.
– конечное число. Тогда оба ряда сходятся или расходятся одновременно.
Пример. Исследовать ряд 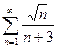 на сходимость.
на сходимость.
Решение. Выберем ряд для сравнения, выяснив для этого, как ведёт себя общий член ряда при больших n:
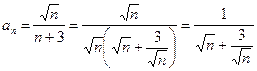 ~
~ 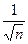 .
.
Т.е. 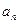 ~
~ 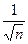 , и в качестве ряда сравнения берём ряд
, и в качестве ряда сравнения берём ряд  , который расходится, что было показано ранее.
, который расходится, что было показано ранее.
Вычислим предел
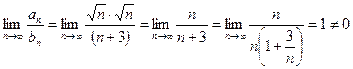 ,
,
и значит, оба ряда ведут себя одинаково, т.е. данный ряд тоже расходится.
Признак Даламбера
Пусть дан ряд 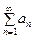 и существует предел
и существует предел 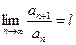 . Тогда, если l < 1, то ряд сходится, если l > 1, то ряд расходится, если l = 1, то этот признак ответа не даёт (т.е. необходимо дополнительное исследование).
. Тогда, если l < 1, то ряд сходится, если l > 1, то ряд расходится, если l = 1, то этот признак ответа не даёт (т.е. необходимо дополнительное исследование).
Пример. Исследовать на сходимость ряд 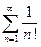 (напомним, что
(напомним, что 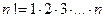 , т.е. n -факториал есть произведение всех целых чисел от 1 до n).
, т.е. n -факториал есть произведение всех целых чисел от 1 до n).
Решение. Для этого ряда 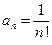 ,
, 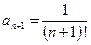 (для нахождения
(для нахождения 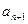 нужно в
нужно в 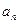 вместо n подставить n + 1). Вычислим предел
вместо n подставить n + 1). Вычислим предел
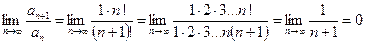 ,
,
и так как предел меньше 1, данный ряд сходится.
Радикальный признак Коши
Пусть дан ряд 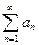 и существует предел
и существует предел 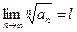 . Если l < 1, то ряд сходится, если l > 1, то ряд расходится, если l = 1, то этот признак ответа не даёт (необходимо дополнительное исследование).
. Если l < 1, то ряд сходится, если l > 1, то ряд расходится, если l = 1, то этот признак ответа не даёт (необходимо дополнительное исследование).
Пример. Исследовать на сходимость ряд 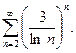
Решение. Общий член ряда 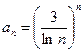 . Вычислим предел
. Вычислим предел 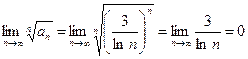 . Значит, ряд сходится.
. Значит, ряд сходится.
Интегральный признак Коши
Рассмотрим ряд 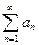 , и предположим, что на промежутке х Î
, и предположим, что на промежутке х Î 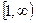 существует непрерывная, положительная и монотонно убывающая функция
существует непрерывная, положительная и монотонно убывающая функция 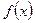 такая, что
такая, что 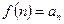 , n = 1, 2, 3…. Тогда ряд
, n = 1, 2, 3…. Тогда ряд 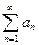 и несобственный интеграл
и несобственный интеграл 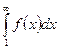 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Отметим, что если дан ряд 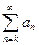 то и функция рассматривается на промежутке
то и функция рассматривается на промежутке 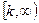 .
.
Напомним, что указанный несобственный интеграл называется сходящимся, если существует конечный предел 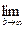
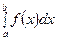 , и тогда
, и тогда 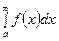 =
=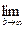
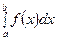 . Если
. Если 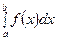 при
при 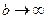 не имеет конечного предела, то говорят, что несобственный интеграл
не имеет конечного предела, то говорят, что несобственный интеграл 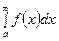 расходится.
расходится.
Пример. Рассмотрим ряд 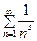 – обобщённый гармонический ряд или ряд Дирихле с показателем степени s. Если s = 1, то ряд
– обобщённый гармонический ряд или ряд Дирихле с показателем степени s. Если s = 1, то ряд 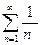 называют гармоническим рядом.
называют гармоническим рядом.
Исследуем данный ряд, используя интегральный признак Коши: 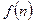 =
=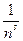 , и функция
, и функция 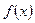 =
=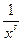 обладает всеми свойствами, указанными в признаке. Вычислим несобственный интеграл
обладает всеми свойствами, указанными в признаке. Вычислим несобственный интеграл 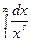 .
.
Возможны три случая:
1) s < 1, и тогда
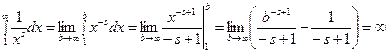 ,
,
интеграл расходится.
2) при s = 1
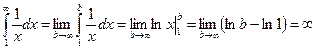 ,
,
интеграл расходится.
3) если s > 1, то
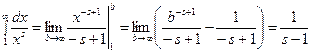 ,
,
интеграл сходится.
Вывод. Обобщенный гармонический ряд 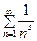 сходится, если s > 1, и расходится, если s ≤ 1.
сходится, если s > 1, и расходится, если s ≤ 1.
Этот ряд часто используют для сравнения с другими рядами, содержащими степени n.
Пример. Исследовать ряд 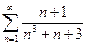 на сходимость.
на сходимость.
Решение. Для этого ряда 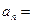
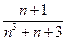 ~
~ 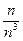 =
=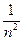 , значит, данный ряд сравниваем с рядом
, значит, данный ряд сравниваем с рядом 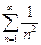 , который сходится, как ряд Дирихле с показателем степени s = 2 > 1.
, который сходится, как ряд Дирихле с показателем степени s = 2 > 1.
По признаку сравнения в предельной форме находим предел отношения общих членов данного ряда и ряда Дирихле:
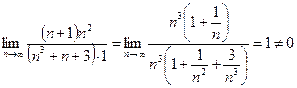
Следовательно, данный ряд тоже сходится.
Рекомендации по использованию признаков сходимости
Прежде всего, следует воспользоваться необходимым признаком сходимости ряда и вычислить предел общего члена ряда при 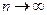 . Если
. Если 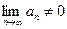 , то ряд заведомо расходится, а если
, то ряд заведомо расходится, а если 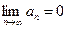 , то следует воспользоваться одним из достаточных признаков.
, то следует воспользоваться одним из достаточных признаков.
Признаки сравнения полезно использовать в тех случаях, когда путём преобразований выражения для общего члена ряда удаётся перейти от исходного ряда к ряду, сходимость (или расходимость) которого известна. В частности, если 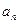 содержит только степени n и не содержит никакие другие функции, это всегда можно сделать.
содержит только степени n и не содержит никакие другие функции, это всегда можно сделать.
Признаки сравнения применяют тогда, когда исходный ряд можно сопоставить с обобщённым гармоническим рядом или рядом, составленным из членов бесконечной геометрической прогрессии.
Пример 1. Исследовать на сходимость ряд:
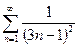 .
.
Решение. Ясно, что при больших n общий член этого ряда сравним с 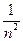 :
: 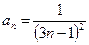 ~
~ 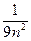 ~
~ 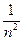 . Значит, рядом сравнения будет обобщённый ряд Дирихле с показателем степени 2:
. Значит, рядом сравнения будет обобщённый ряд Дирихле с показателем степени 2: 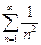 , который сходится, т.к. s = 2 > 1.
, который сходится, т.к. s = 2 > 1.
Вычислим предел
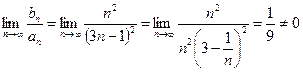 .
.
Значит, данный ряд тоже сходится.
Пример 2. Исследовать сходимость ряда 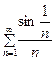 .
.
Решение. Так как при х > 0, sin x < х (см. рис. 2), то 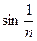 <
< 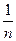 , значит,
, значит, 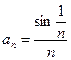 <
<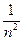 .
.
Поскольку ряд 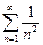 с бóльшими членами сходится, значит, данный ряд тоже сходится.
с бóльшими членами сходится, значит, данный ряд тоже сходится.
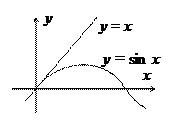
Рис 2. Графики функций х и sin x
Признак Даламбера удобно применять, когда 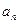 содержит показательную функцию, факториал n! или то и другое.
содержит показательную функцию, факториал n! или то и другое.
Пример 3. Исследовать на сходимость ряд 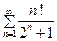 .
.
Решение. Так как 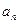 содержит n!, то удобно воспользоваться признаком Даламбера. Общий член ряда равен
содержит n!, то удобно воспользоваться признаком Даламбера. Общий член ряда равен 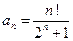 , и значит,
, и значит, 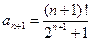 . Предел отношения этих членов ряда равен
. Предел отношения этих членов ряда равен
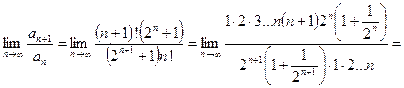
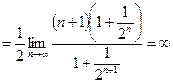 ,
,
т.к. при 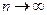 :
: 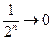 ,
, 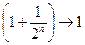 ,
, 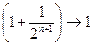 ,
, 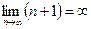 . Раз предел больше единицы, значит, ряд расходится.
. Раз предел больше единицы, значит, ряд расходится.
Радикальный признак Коши следует применять, если общий член ряда имеет вид 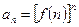
Пример 4. Исследовать ряд 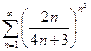 на сходимость.
на сходимость.
Решение. Здесь общий член ряда 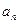 =
=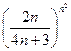 , и удобно применить признак Коши. Вычислим предел:
, и удобно применить признак Коши. Вычислим предел: 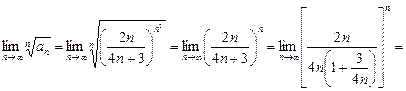
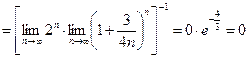 .
.
Значит, данный ряд сходится.
Интегральный признак Коши применяют, если при замене 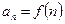 получается функция
получается функция 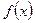 , интеграл от которой вычисляется достаточно просто.
, интеграл от которой вычисляется достаточно просто.
Пример 5. Исследовать сходимость ряда 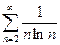 .
.
Решение. Воспользуемся интегральным признаком, взяв в качестве функции 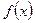 =
=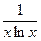 , которая на промежутке
, которая на промежутке 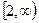 является положительной, непрерывной и монотонно убывающей, и
является положительной, непрерывной и монотонно убывающей, и 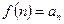 .
.
Вычислим несобственный интеграл:
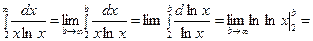
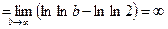 .
.
Интеграл расходится, значит, ряд тоже расходится.
Для предварительной оценки сходимости заданного ряда полезно иметь в виду, как быстро растут разные функции с ростом n. Самой медленно растущей функцией является логарифм, а быстрее всего растёт степенно-показательная функция 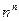 . Между ними другие известные функции располагаются в следующем порядке:
. Между ними другие известные функции располагаются в следующем порядке:
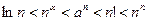 .
.
Поэтому, если в числителе стоит какая-то из этих функций, а в знаменателе - функция левее её, то, скорее всего, ряд расходится, и наоборот.
 2014-01-25
2014-01-25 1503
1503