Каждое алгебраическое уравнение имеет во множестве комплексных чисел по крайней мере один корень.
Для уравнений третьей и четвертой степени формулы корней громоздки и ими предпочитают не пользоваться. А для уравнений степени выше четвертой подобных формул в общем случае не существует.
Для решения уравнений с целыми коэффициентами часто оказывается полезной следующая теорема:
Пример. Решить уравнение 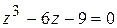 .
.
Рассматривая делители свободного члена, убеждаемся в том, что только 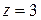 является целым корнем уравнения. Делим левую часть уравнения на
является целым корнем уравнения. Делим левую часть уравнения на 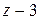 :
:
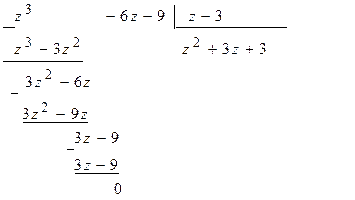
Поэтому 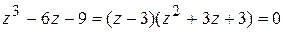 . Решая квадратное уравнение
. Решая квадратное уравнение 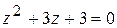 , получаем все остальные корни:
, получаем все остальные корни:
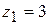 ,
, 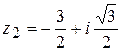 ,
, 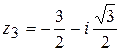 .
.
 2014-01-25
2014-01-25 796
796








