2014-01-25
1130
Рассмотрим алгебраические уравнения степени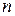 
с комплексными коэффициентами: 
.
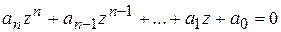Число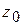 
называется решением или корнем уравнения, если при постановке 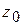в уравнение получается верное числовое равенство.
Решить уравнение во множестве комплексных чисел – значит, найти все его корни.
Рассмотрим решение таких уравнений.
1. Уравнение первой степени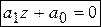 
, 
.
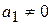Пример. Решить уравнение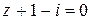 
.
Уравнение 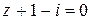имеет один корень 
.
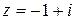2. Уравнение второй степени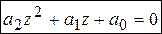 
, 
.
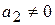Пример. Решить уравнение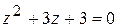 
.
,
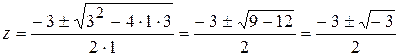Учитывая, что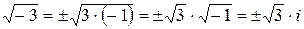 
, получаем два комплексных корня:
, 
.
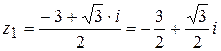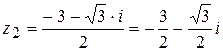Пример. Найти корни уравнения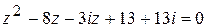 
.
Перепишем уравнение в удобном виде: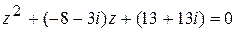 
.
В формуле для корней квадратного уравнения нет символа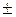 
, а только 
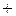, поэтому:
.
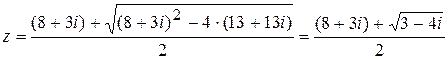Для определения всех значений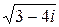 
положим 
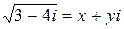, тогда 
, 
.
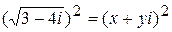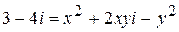Следовательно,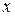 
и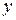 
удовлетворяют системе уравнений 
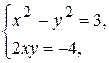причем 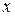и 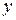- действительные числа.
Система имеет два действительных решения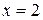 
, 
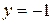и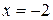 
, 
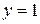. Поэтому 
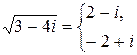и
, 
.
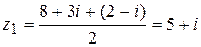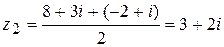3. Уравнение третьей степени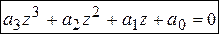 
, .
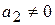В 1799 г. великим математиком Карлом Гауссом была доказана теорема (называется основной теоремой алгебры):
