Вынужденные колебания
Рассмотрим теперь случай, когда в системе наряду с силами упругости и трения присутствует некоторая внешняя сила, препятствующая затуханию колебаний. Предположим, что эта вынуждающая сила Fв действует периодически с круговой частотой wв и зависит от времени по закону: Fв = Fо sin wв t, где Fо - амплитуда вынуждающей силы.
Для этого случая дифференциальное уравнение (второй закон Ньютона) имеет вид:
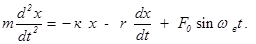 (13)
(13)
Сохраняя обозначения к / m = w 02 , r / m = 2b, и обозначив F0 /m = f0 приведем уравнение (13) к виду:
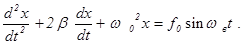 (14)
(14)
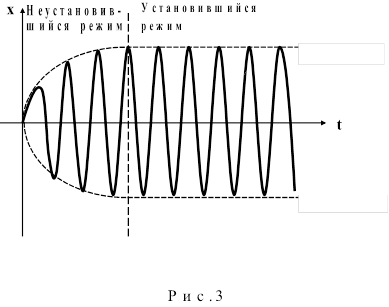 |
Решение этого уравнения представляет некоторую функцию, которая графически представлена на рис. 3. Это решение состоит из двух частей. Одна из них соответствует неустановившемуся режиму колебаний, когда их амплитуда зависит от времени. Вторая часть описывает установившийся режим колебаний.
В установившемся режиме вынужденных колебаний смещение х подчиняется гармоническому закону и происходит с частотой, равной частоте действия вынуждающей силы:
х = А sin (w в t + jo). (15)
Установившаяся амплитуда А вынужденных колебаний, зависит от параметров системы (частоты собственных колебаний w 0 и коэффициента затухания b) и от характеристик вынуждающей силы (f0 и wв): А = f (w0,b, f0,w в). Строгое рассмотрение приводит к следующим выражением для значений А и j0, входящих в формулу (15):
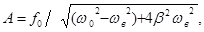 (16)
(16)
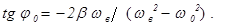 (17)
(17)
Из рассматриваемой формулы (16) следует, что амплитуда достигает максимального значения Аmах при определенном соотношении между величинами w0,w в и b.
Минимум знаменателя в формуле (16) достигается при условии:
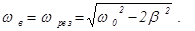 (18)
(18)
То есть, амплитуда вынужденных колебаний максимальна, если частота действия вынуждающей силы определяется формулой (18). Явление резкого возрастания амплитуды вынужденных колебаний при частоте действия вынуждающей силы, определяемой формулой (16), называется резонансом.
Если бы затухание в системе отсутствовало (b = 0), то резонанс наступал бы при условии (w0 = w в) и при этом амплитуда достигала бы бесконечно большого значения.
 2014-01-25
2014-01-25 2804
2804
