Лекция 15 Электромагнитные колебания и волны

1. Колебательный контур. Свободные и вынужденные электромагнитные колебания.

2. Переменный электрический ток. Закон Ома для переменного тока.

Тезисы

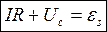
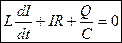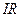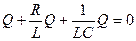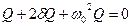1. Свободные затухающие коле­бания — колебания, амплитуда которых из-за потерь энергии реальной колебатель­ной системой с течением времени умень­шается. Закон затухающих колебаний опреде­ляется свойствами колебательных систем. Закон Ома для контура RLC , где - напряжение на резисторе. Дифференциальное уравнение свобод­ных затухающих колебаний заряда в контуре или , где 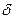- коэффициент затухания, равный 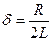. Его решение 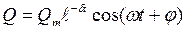. Затухающие колеба­ния не являются периодическими (рис. 208).

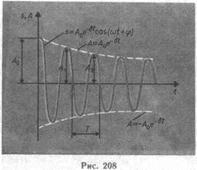
Амплитуда затухающих колебаний 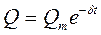. Циклическая частота 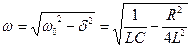, период 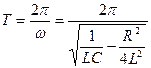. Характеристиками колебательных систем являются декремент затухания, время релаксации, логарифмический декремент затухания, добротность системы.

Если A(t) и A(t+T) — амплитуды двух последовательных колебаний, соответству­ющих моментам времени, отличающимся на период, то отношение 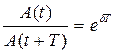называется декрементом затухания, а его логарифм 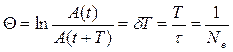— логарифмическим декрементом затуха­ния; N_e — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Промежуток времени, в течение которого амплитуда за­тухающих колебаний уменьшается в е раз, называется временем релаксации 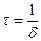. Добротно­сть колебательной системы 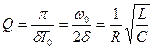Электрический резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешней ЭДС к частоте, равной или близкой собственной частоте колебательного контура. Зависимость амплитуды колебаний заряда на конденсаторе от частоты 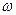внешней ЭДС 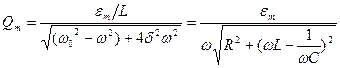, где 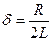, 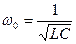. 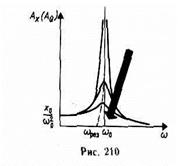Резонансная частота – частота, при которой амплитуда достигает максимального значения 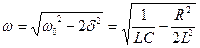. Зависимость амплитуды заряда на конденсаторе от частоты внешней ЭДС при различных коэффициентах затухания (рис. 210). При 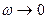все кривые достигают статического отклонения 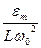, а при 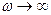- асимптотически стремятся к нулю. Чем больше 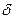, тем ниже и левее максимумы резонансных кривых.

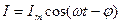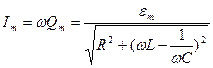2. Сила тока при установившихся вынужденных колебаниях , где амплитуда тока, 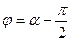- сдвиг по фазе между током и внешней ЭДС. Резонансная частота для силы тока 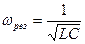. Резонансные кривые для амплитуды силы тока - рис. 211. Амплитуда силы тока максимальна при 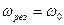и равна 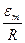. Чем больше коэффициент затухания 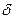, тем ниже максимум.

Электрический ток, величина и направление которого изменяются во времени, есть переменный ток. Установившиеся электромагнитные вынужденные колебания можно рассматривать как протекание переменного тока в цепи. Цепь переменного тока - цепь, содержащая резистор, катушку индуктивности и конденсатор, к которому приложено переменное напряжение.

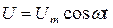
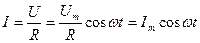
1 .Переменный ток, текущий через ре­зистор сопротивлением R (L®0, С®0). При выполнении условия квазистационарности ток через резистор определяется законом Ома: 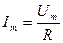- амплитуда силы тока )

2. Переменный ток, текущий через конденсатор. Падение напряжения на конденсаторе 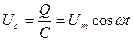. Сила тока 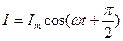, где амплитуда силы тока 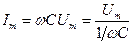, а величина 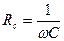есть реактивное емкостное сопротивление. Для постоянного тока R_C=¥, он через конденсатор течь не может. Падение напряжения на конденсаторе 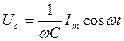Падение напряже­ния U_C отстает по фазе от текущего через конденсатор тока I на p/2.

3. Переменный ток, текущий через ка­тушку. ЭДС самоиндукции 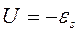. Закон Ома 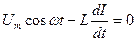Падение напряжения на катушке 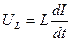Сила тока 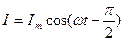, где 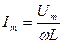- амплитудное значение силы тока, 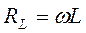- реактивное индуктивное сопротивление. Падение напряжения на катушке 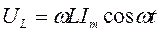. Для постоянного тока катушка не имеет сопротив­ления. Падение напряже­ния U_L опережает по фазе ток I, текущий через катушку, на p/2. Для активного сопротивления 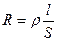– график 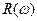есть прямая, параллельная оси 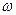, для индуктивного сопротивления 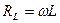- график 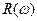есть прямая пропорциональность, для емкостного сопротивления 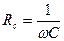- график 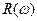есть обратная пропорциональность. Условие резонанса 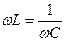, , 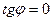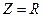Резонансная частота 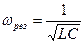Средняя мощность 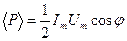, 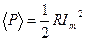.Действующее значение тока 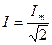и напряжения 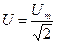Средняя мощность 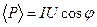, коэффи­циент мощности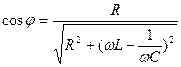

Основная литература

1. Трофимова Т.И. Курс физики. – М.: ACADEMIA, 2007. – 558 с.

2. Савельев И.В. Курс общей физики: в 5 кн.; Астрель: АСТ, 2005. – М., 1 кн, 2 кн, 3 кн.

3. Детлаф А.А. Курс физики. – М.: ACADEMIA, 2008. – 720 с.

4. Пономаренко Е.В. Физика: Уч. пособие. – Шымкент: ЮКГУ им. М.Ауезова, 2012. – 176 с.

5. Трофимова Т.И. Сборник задач по курсу физики для вузов. – М.: Оникс 21 век, 2005. – 384 с.

6. Волькенштейн В.С. Сборник задач по курсу физики. – СПб.: Книжный мир, 2007. – 328 с.

7. Иродов И.Е. Задачи по общей физике. – М.: Бином. Лаборатория знаний, 2007. – 416 с.