Формулы для скорости и ускорения при круговом движении точки

Дадим теперь выражения для скорости 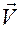и ускорения 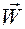в круговом движении. Согласно выводам §2, скорость 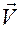и ускорение 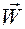будут вычисляться по формулам

, ,

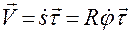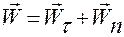где

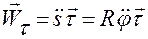— касательное ускорение,

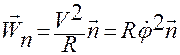— нормальное ускорение.

Введем обозначения

, .

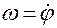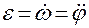Тогда выражения для векторов 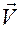, , 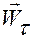, 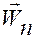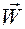и их модулей примут следующий вид:

, ;

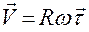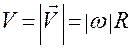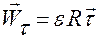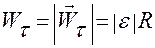, ; (1.3.14)

, ,

, .

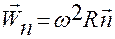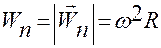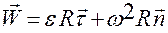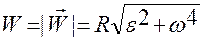Если введем векторы

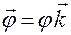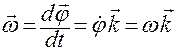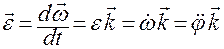, , , (1.3.15)

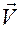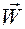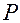то через них скорость и ускорение точки в круговом движении можем записать в следующей форме:

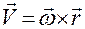, (1.3.16)

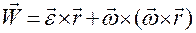. (1.3.17)

Соотношение (1.3.16) называется формулой Эйлера для кругового движения материальной точки.

Соотношение (1.3.17) называется формулой Ривальса для ускорения материальной точки в круговом движении.

Справедливость формул (1.3.16), (1.3.17) легко устанавливается, если подставить в их левые части соотношения (1.3.14) для векторов 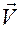и 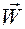, а в правые — соотношения (1.3.15), (1.3.12), (1.3.13):

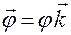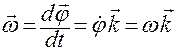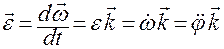, , , (1.3.15)

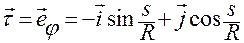. (1.3.12)

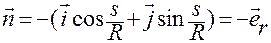. (1.3.13)

и учесть очевидные равенства

, , ,

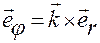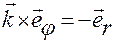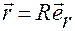которые выполняются на кругового движении.

Для векторов 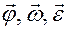приняты следующие названия:

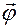— вектор углового поворота точки в круговом движении;

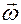— вектор мгновенной угловой скорости кругового движения точки;

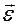— вектор мгновенного углового ускорения в круговом движении точки.

Из (1.3.15)

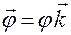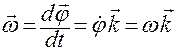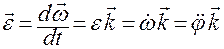, , , (1.3.15)

следует, что в любой момент времени 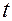вектора 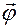, 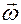и 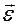ортогональны плоскости движения материальной точки.