Репер Френе при круговом движении точки

Построим явные зависимости ортов 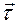и 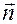репера Френе от радиуса 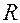и длины дуги 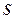на круговом движении.

Согласно формулам Френе, имеем

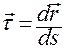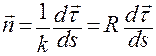, , (1.3.10)

где 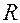— радиус кривизны.

Здесь воспользовались известным соотношением

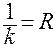
для окружности.

После подстановки (1.3.6),(1.3.7):

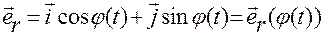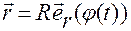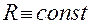, ,,(1.3.6)

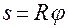, (1.3.7)

в формулу для направляющего вектора 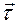касательной находим

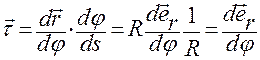. (1.3.11)

Далее, введя обозначение

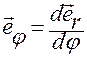
и подставляя в него (1.3.6)

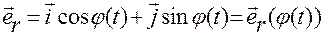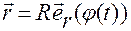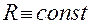, ,,(1.3.6)

получим зависимость орта 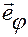от угла в следующем виде:

.

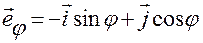А тогда, учитывая равенства (1.3.11) и (1.3.7):

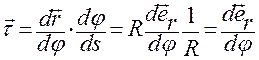, (1.3.11)

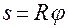, (1.3.7)

окончательно для орта 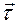будем иметь

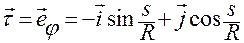. (1.3.12)

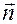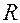Зависимость орта от и 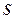получим, подставив орт 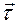из (1.3.12) во вторую формулу Френе (1.3.10):

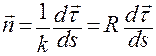, (1.3.10)

После дифференцирования по 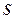выражение для вектора 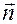примет вид

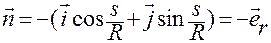. (1.3.13)

Формулы (1.3.12) и (1.3.13) позволяют вычислить два орта репера Френе в любой точке окружности.

Третий вектор репера Френе – орт бинормали совпадает с ортом 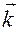. Он не зависит от положения точки на окружности.