Определение 1

Определение криволинейных координат точки

Криволинейными или, иначе, обобщенными координатами материальной точки будем называть три независимые величины 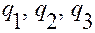, которые обладают следующими свойствами.

1. Для любых значений 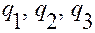из некоторой области 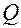трехмерного пространства переменных 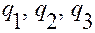определена однозначная, дважды непрерывно дифференцируемая вектор-функция 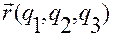, такая, что ее векторное значение

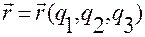(1.5.1)

задает положение материальной точки в абсолютном

пространстве при .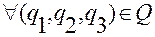

2. Для любого положения материальной точки в абсолютном пространстве можно поставить в соответствие одно и только одно значение переменных .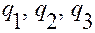

3. При любых значениях 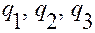из области 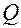смешанное произведение векторов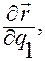 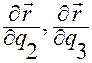не равно нулю, т.е.

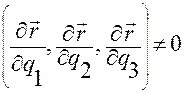. (1.5.2)