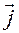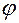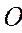Задание движения точки в полярных координатах
При описании кругового движения точки использовалось представление этого движения через закон изменения угла  и закон изменения (точнее сказать, закон сохранения неизменным) расстояния от точки отсчета
и закон изменения (точнее сказать, закон сохранения неизменным) расстояния от точки отсчета 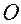 до геометрической точки
до геометрической точки 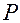 , с которой в момент времени
, с которой в момент времени 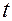 по положению совпадает материальная точка.
по положению совпадает материальная точка.
Иначе говоря, при описании движения точки использовались две переменные: 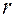 и
и  .
.
Такие переменные 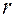 и
и  , как правило, наиболее часто применяются для описания плоского движения материальной точки. Их называют координатами точки в полярной системе координат.
, как правило, наиболее часто применяются для описания плоского движения материальной точки. Их называют координатами точки в полярной системе координат.
1º. Понятие полярной системы координат
Полярная система координат задается следующим образом (см. рис.1.4.1):
· фиксируем в плоскости движения точку отсчета 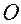 и ось
и ось 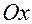 , проходящую через точку отсчета;
, проходящую через точку отсчета;
· задаем положительное направление отсчета расстояний от точки 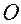 вдоль этой оси; это направление совпадает с направлением орта
вдоль этой оси; это направление совпадает с направлением орта 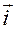 .
.
Положительная полуось 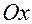 называется полярной осью.
называется полярной осью.
Пусть в некоторый момент времени 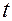 материальная точка
материальная точка 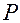 занимает на плоскости положение
занимает на плоскости положение 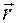 , где
, где 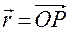 .
.
Будем определять это положение расстоянием 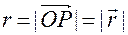 от точки
от точки 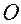 до точки
до точки 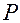 и углом
и углом  , который образует вектор
, который образует вектор 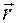 с полярной осью.
с полярной осью.
Угол  отсчитываем от полярной оси
отсчитываем от полярной оси 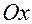 до вектора
до вектора 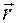 .
.
Положительным направлением отсчета угла  считается направление против часовой стрелки, если смотреть с конца орта
считается направление против часовой стрелки, если смотреть с конца орта 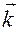 , выбранного для ориентации данной плоскости и ортогонального ей.
, выбранного для ориентации данной плоскости и ортогонального ей.
Построенная таким образом система координат называется полярной системой, а координаты 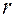 и
и  называются полярными координатами точки.
называются полярными координатами точки.
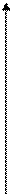

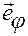

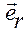

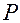
|
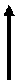
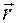
|
|


|


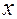

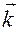
полярная ось
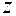
Рис.1.4.1
Введем декартовую прямоугольную систему координат 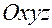 , в которой (см. рис.1.4.1):
, в которой (см. рис.1.4.1):
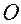 — точка отсчета совпадает с полюсом
— точка отсчета совпадает с полюсом
полярной системы;
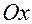 — совпадает с полярной осью;
— совпадает с полярной осью;
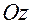 — ортогональна плоскости движения, и орт
— ортогональна плоскости движения, и орт 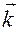
является ее базисным вектором,
определяющим ориентацию плоскости 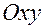 ;
;
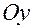 — дополняет систему
— дополняет систему 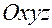 до правой.
до правой.
Тогда связь декартовых и полярных координат точки задается очевидным соотношением
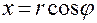 ,
, 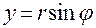 ,
, 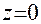 . (1.4.1)
. (1.4.1)
Здесь 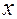 ,
,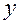 ,
,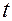 — декартовые координаты точки
— декартовые координаты точки 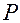 ;
; 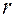 и
и  — ее полярные координаты, причем
— ее полярные координаты, причем 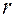 и
и  изменяются в пределах
изменяются в пределах 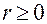 и
и 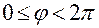 .
.
Из (1.4.1) вытекает, что 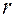 и
и  однозначно определяют координаты
однозначно определяют координаты 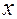 и
и 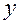 точки
точки 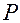 в плоскости
в плоскости 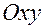 .
.
Из них легко получить обратную зависимость, т.е. зависимость полярных координат 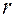 и
и  точки
точки 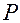 от ее декартовых координат
от ее декартовых координат 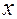 и
и 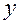 ,
,
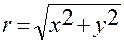 ,
, 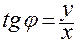 . (1.4.2)
. (1.4.2)
Второе равенство в (1.4.2) справедливо только при 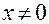 .
.
Если 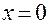 ,
, 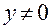 , то из первого равенства в (1.4.1) получаем
, то из первого равенства в (1.4.1) получаем 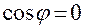 . А тогда с учетом второго равенства в (1.4.1) будем иметь:
. А тогда с учетом второго равенства в (1.4.1) будем иметь:
· если 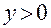 , то
, то 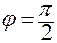 ;
;
· если 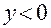 , то
, то 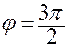 .
.
Если 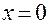 и
и 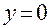 , то
, то 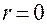 , и угол
, и угол  может принимать любые значения.
может принимать любые значения.
Таким образом, если 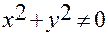 , то по координатам
, то по координатам 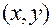 точки
точки 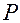 однозначно определяются ее полярные координаты
однозначно определяются ее полярные координаты 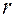 и
и  :
:
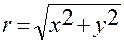 ,
, 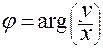 ,
,
где функция 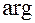 называется функцией аргумент.
называется функцией аргумент.
Она имеет следующую аналитическую структуру:
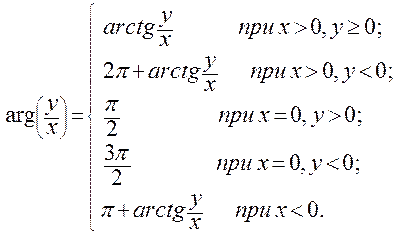
Функция 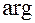 не определена в точке
не определена в точке 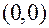 и однозначна во всех остальных точках плоскости
и однозначна во всех остальных точках плоскости  .
.
2º. Задание движения в полярных координатах
Задать движение в полярных координатах — это значит:
· задать закон изменения координат 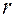 и
и  по времени
по времени
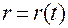 ,
, 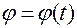 (1.4.3)
(1.4.3)
в вектор-функции 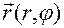 .
.
Вектор-функция 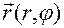 устанавливает связь положения
устанавливает связь положения 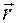 точки с ее полярными координатами
точки с ее полярными координатами 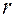 и
и  .
.
Эта связь в векторной форме имеет вид
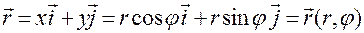 .
.
Введем орты 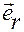 и
и 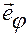 , вычисляемые через полярные координаты точки
, вычисляемые через полярные координаты точки 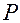 .
.
Положим, по определению,
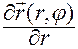
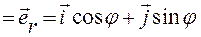 ,
,
(1.4.4)
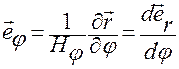
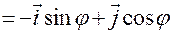 ,
,
где
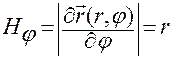 .
.
Очевидно:
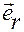 — это орт радиус-вектора
— это орт радиус-вектора 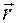 точки
точки 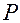 ,
,
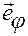 — орт, показывающий направление
— орт, показывающий направление
возрастания угла  .
.
Иначе,
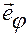 – это орт касательной к окружности радиуса
– это орт касательной к окружности радиуса 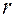
с центром в точке 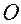 (орт касательной в точке
(орт касательной в точке 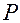 ).
).
Орты 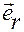 и
и 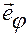 взаимно ортогональны.
взаимно ортогональны.
Векторы 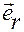 и
и 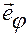 называются базисом полярной системы координат.
называются базисом полярной системы координат.
Используя закон движения (1.4.3)
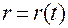 ,
, 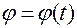 (1.4.3)
(1.4.3)
и первое соотношение в (1.4.4)
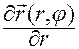
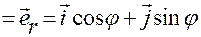 ,
,
(1.4.4)
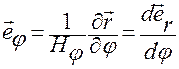
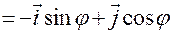 ,
,
получим
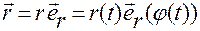 . (1.4.5)
. (1.4.5)
Формула (1.4.5) — это векторный способ задания движения через полярные координаты.
В ней
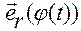
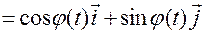 .
.
3º. Скорость точки в полярных координатах
Дифференцируя (1.4.5), получим
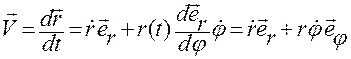 . (1.4.6)
. (1.4.6)
Формула (1.4.6) дает разложение вектора скорости 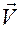 по базису полярной системы координат.
по базису полярной системы координат.
Отсюда следует, что
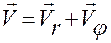 ,
, 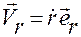 ,
, 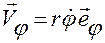 ,
,
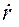 и
и 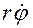 — полярные координаты скорости.
— полярные координаты скорости.
Вектор 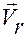 называется радиальной скоростью, а
называется радиальной скоростью, а 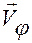 — трансверсальной скоростью точки.
— трансверсальной скоростью точки.
Учитывая ортогональность ортов 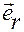 и
и 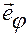 , из (1.4.6) находим выражение для модуля
, из (1.4.6) находим выражение для модуля 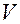 скорости
скорости 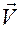 :
:
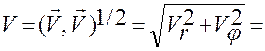
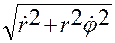 .
.
4º. Ускорение точки в полярных координатах.
Дифференцируя (1.4.6) по времени 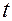 , получим
, получим
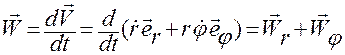 , (1.4.7)
, (1.4.7)
где
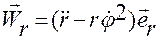 ,
, 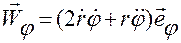 .
.
Вектор 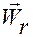 называется радиальным ускорением точки, а вектор
называется радиальным ускорением точки, а вектор 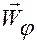 — трансверсальным ускорением точки.
— трансверсальным ускорением точки.
Из (1.4.6) и (1.4.7) легко получить формулы для скорости и ускорения в круговом движении с учетом того, что на таком движении выполняются тождества 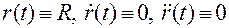 .
.
§5. Задание движения материальной точки
в криволинейных координатах
1º. Понятие криволинейных (обобщенных)
координат точки
 2014-01-25
2014-01-25 814
814