(шесть уравнений статики абсолютно твердого тела)
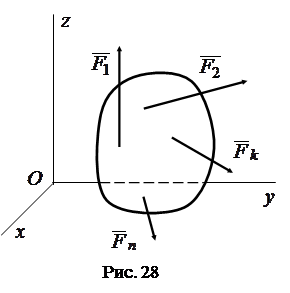 |
Пусть на твердое тело, находящееся в равновесии, действует система сил
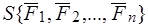 (рис. 28).
(рис. 28). Выберем произвольную систему координат и обозначим проекции сил на оси координат:
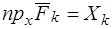 ,
, 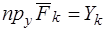 ,
, 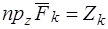
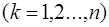 .
.
Главный вектор этой системы сил:
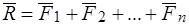 .
.
Его проекции на оси координат:
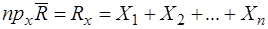 ,
,
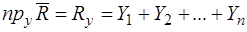 ,
,
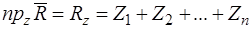 .
.
Главный момент вычислим относительно полюса, находящегося в начале координат:
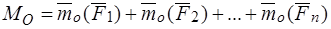 .
.
Главный момент относительно полюса в начале координат проектируем на каждую из осей координат:
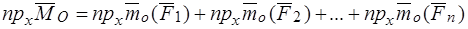 .
.
На основании теоремы о связи между моментами силы относительно полюса и оси:
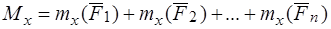 ,
,
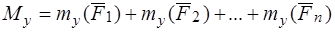 ,
,
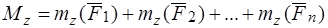 .
.
По основной теореме статики для равновесия тела под действием произвольной системы сил необходимо и достаточно, чтобы были равны нулю главный вектор и главный момент относительно произвольного полюса, то есть
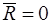 , (I)
, (I) 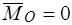 , (II)
, (II)
Векторное равенство (I) эквивалентно трем скалярным:
1. 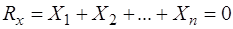 ,
,
2. 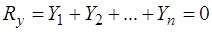 ,
,
3. 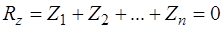 .
.
Векторное равенство (II) так же эквивалентно трем скалярным:
4. 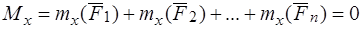 ,
,
5. 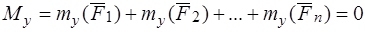 ,
,
6. 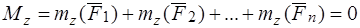 .
.
На основании полученного результата основная теорема статики может быть сформулирована так:
|
|
|
Для того, чтобы твердое тело под действием произвольной системы сил находилось в равновесии необходимо и достаточно, чтобы сумма проекций всех сил на каждую из осей координат и сумма моментов всех сил относительно каждой из осей координат равнялась нулю, то есть чтобы выполнялись шесть уравнений статики:
1. 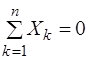 , 4.
, 4. 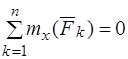 ,
,
2. 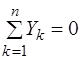 , 5.
, 5. 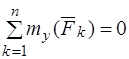 ,
,
3. 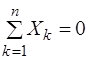 , 6.
, 6. 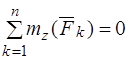 .
.
 2014-01-25
2014-01-25 1172
1172







