Теорема. Если система сил имеет равнодействующую, то момент этой равнодействующей относительно некоторого полюса равен геометрической сумме моментов всех сил системы относительно того же полюса.
Дано: 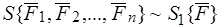 .
.
Требуется доказать, что: 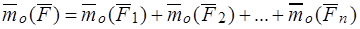 .
.
Доказательство. В силу второго свойства элементарных операций главные моменты 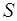 и
и 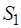 равны:
равны:
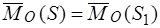 ,
,
или 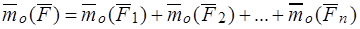 .
.
Теорема Вариньона, доказанная для момента равнодействующей относительно полюса, остается справедливой и для момента равнодействующей относительно оси.
Теорема. Если система сил имеет равнодействующую, то момент этой равнодействующей относительно некоторой оси равен алгебраической сумме моментов всех сил системы относительно той же оси.
Доказательство:
Пусть 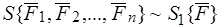 . Тогда:
. Тогда:
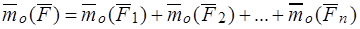 .
.
Спроектируем это векторное равенство на ось 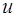 , проходящую через полюс:
, проходящую через полюс:
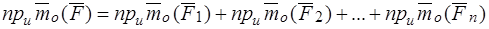 .
.
В силу теоремы о связи между моментом силы относительно полюса и моментом силы относительно оси:
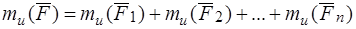 .
.
 2014-01-25
2014-01-25 782
782








