ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ.
Равнодействующая системы сходящихся сил находится с помощью сложения сил по правилу параллелограмма. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку. Такой метод дает лемма Пуансо.
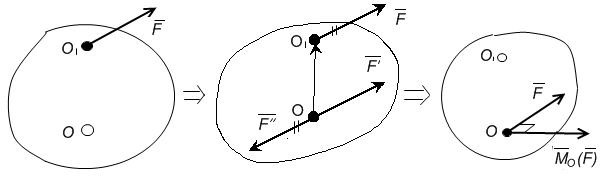 |
Сил а 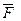 , приложенная в точке О1, эквивалентна геометрически равной ей силе , приложенная в точке О1, эквивалентна геометрически равной ей силе 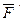 в точке О и паре сил с моментом, равным моменту силы в точке О и паре сил с моментом, равным моменту силы 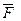 относительно точки О. Пусть сила относительно точки О. Пусть сила 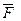 приложена в точке О1. Действие этой силы не изменяется, если в точке О приложить две уравновешенные силы, равные по модулю F. Полученная система трех сил представляет собой силу приложена в точке О1. Действие этой силы не изменяется, если в точке О приложить две уравновешенные силы, равные по модулю F. Полученная система трех сил представляет собой силу 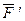 равную равную 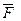 , но приложенную в точке О и пару , но приложенную в точке О и пару 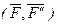 с моментом с моментом 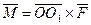 . . |
Операция замены силы 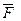 силой
силой 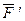 и парой сил
и парой сил 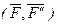 называется приведением силы
называется приведением силы 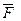 к заданному центру. Возникающая пара сил называется присоединенной.
к заданному центру. Возникающая пара сил называется присоединенной.
Основная теорема статики
Применяем теорему Пуансо к произвольной системе сил. Пусть точка О – центр приведения.
1) Выполняем параллельный перенос всех сил в точку О и получаем ССС. Находим геометрическую сумму всех сил - главный вектор СС.
Главным вектором системы сил называется вектор, равный векторной сумме этих сил.
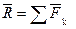 .
.
2) В точке О прикладываем вектор-моменты всех сил, равные моментам всех присоединенных ПС, и получаем вторую систему сходящихся векторов. Выполняем операцию геометрического сложения и находим главный момент СС относительно центра приведения.
Главным моментом системы сил относительно точки О тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.
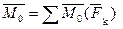
Основная теорема статики. Произвольная система сил при приведении к выбранному центру О эквивалентна одной силе, равной главному вектору системы сил, и одной паре сил с моментом, равным главному моменту системы сил относительно центра приведения.
Операция приведения к центру называется приведением СС к простейшему виду.
Определение главного вектора и главного момента системы сил
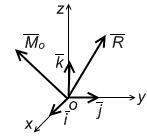 | Главный вектор и главный момент определяются в декартовых координатах с помощью проекций: 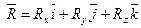 , , 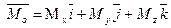 . . |
Проекции векторов на оси координат:
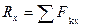 ,
, 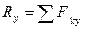 ,
, 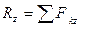
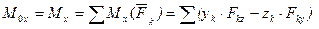 ,
,
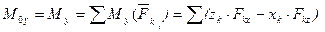 ,
,
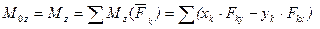 .
.
 2014-01-25
2014-01-25 1990
1990








