МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
УЖГОРОДСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
ФІЗИЧНИЙ ФАКУЛЬТЕТ
ЖИХАРЄВ В.М., КОВАЧ Є.Т.,
ХАРХАЛІС Л.Ю., БЕРЧА Д.М.
МЕХАНІКА
Фізичний практикум
УЖГОРОД - 2007
МЕХАНІКА, Фізичний практикум: Навчальний посібник/ ЖИХАРЄВ В.М., КОВАЧ Є.Т., ХАРХАЛІС Л.Ю., БЕРЧА Д.М. - Ужгород, УжНУ, 2007, -154с.
Рецензент: доктор фізико-математичних наук, професор Попик Ю.В.
У посібнику наведено опис лабораторних робіт, які відповідають курсу “МЕХАНІКА” дисципліни “Загальна фізика” для фізичних факультетів університетів.
Для студентів, які навчаються по напрямку підготовки спеціалістів “Прикладна фізика” та “Фізика”. Буде корисним і для студентів інших спеціальностей.
Ó2007. ЖИХАРЄВ В.М., КОВАЧ Є.Т., ХАРХАЛІС Л.Ю.,БЕРЧА Д.М.
Вступ
Оскільки курс “Механіка” є експериментальним, він повинен ознайомити студента з основними методами спостережень, вимірювань і експериментування. Тому курс супроводжується лабораторними заняттями в загальному фізичному практикумі.
Нижче наводимо тематику лабораторних занять.
1. Вступ, організаційні питання, правила техніки безпеки, значення фізичного експерименту. Загальна характеристика фізичних вимірювань. Систематичні похибки вимірювань.
2. Основи теорії випадкових похибок вимірювань. Прямі вимірювання. Лабораторна робота №1. Експериментальне визначення функцій розподілу випадкових величин.
3. Основи теорії випадкових похибок вимірювань. Непрямі вимірювання. Аналітична обробка результатів вимірювань з допомогою мікроЕОМ, на яких можна програмувати.
4. Лабораторна робота №2. Вимірювання лінійних розмірів і визначення об’ємів твердих тіл.
5. Графічна обробка експериментальних результатів. Лабораторна робота №3. Вивчення систематичних і випадкових похибок на прикладі вимірювання питомого опору ніхромової дротини.
6. Необхідне число вимірювань. Похибка похибки. Повторення матеріалу з теорії похибок. Контрольна робота.
7. Лабораторна робота №4. Вивчення законів прямолінійного руху на машині Атвуда.
8. Лабораторна робота №5. Визначення густини твердих тіл.
9. Лабораторна робота №6. Визначення прискорення сили земного тяжіння за допомогою математичного маятника.
10. Лабораторна робота №7. Визначення прискорення сили земного тяжіння за допомогою оборотного маятника.
11. Лабораторна робота №8. Визначення модуля Юнга за розтягом дротини та прогином стержня.
12. Лабораторна робота №9. Визначення коефіцієнта сили сухого тертя (тертя кочення)
13. Лабораторна робота №10. Вивчення законів обертового руху за допомогою маятника Обербека.
14. Лабораторна робота №11. Визначення еліпсоїда інерції твердих тіл за допомогою крутильних коливань.
15. Лабораторна робота №12. Визначення моменту інерції металевих кілець за допомогою маятника Максвелла.
16. Лабораторна робота №13. Визначення моментів інерції та перевірка теореми Гюйгенса-Штейнера методом крутильних коливань.
17. Лабораторна робота №14. Визначення швидкості куль з допомогою балістичного крутильного маятника.
18. Лабораторна робота №15. Вивчення законів збереження за допомогою зіткнення тіл.
19. Лабораторна робота №16. Вивчення коливань зв’язаних систем.
20. Лабораторна робота №17. Рух тіл при наявності аеродинамічних сил опору.
21. Лабораторна робота №18. Вивчення прецесії вільного гіроскопа.
22. Лабораторна робота №19. Визначення швидкості звуку акустичним методом.
Мета проведення лабораторних занять - ознайомлення з основними методиками вимірювання фізичних величин, приладами і установками, набуття навиків проведення експерименту й обробки експериментальних результатів, поглиблення знань і розуміння суті фізичних явищ і законів.
Завдання проведення лабораторних робіт. У результаті проведення лабораторних занять студент повинен:
- знати суть фізичних законів і понять, основи експериментальних методик, їх чутливість і точність, основи теорії похибок.
- вміти критично аналізувати і виконувати всі етапи лабораторної роботи, вірно використовувати методи наближених обчислень, найбільш поширені засоби обчислювальної техніки для підрахунку результатів експериментальних вимірювань, робити виводи формул абсолютної і відносної похибок для різних випадків, правильно оформляти одержані експериментальні результати і звіт про виконану роботу, скласти коротке резюме по кожному завданню.
Підготовка до лабораторних робіт, їх виконання, оформлення звітів передбачають велику самостійну працю як вдома, так і при роботі в лабораторії. Перш ніж приступити до виконання лабораторної роботи, студент повинен підготувати теоретичні питання, що запропоновані у методичному посібнику до даної лабораторної роботи, вивчити експериментальну установку та суть фізичного явища, вивести робочі формули, вміти оцінити похибки вимірювань. Після допуску викладачем до виконання роботи студент зобов’язаний вести чітко записи в робочому зошиті і на протязі заняття не тільки виконати вимірювання по лабораторній роботі, але й провести обчислення вимірюваної величини і оцінити похибку вимірювань [1-4]. Під час самопідготовки студент оформляє звіт про виконану лабораторну роботу і знайомиться з установками, методичними матеріалами до наступної лабораторної роботи [2-6], вивчає теоретичний матеріал [1,7-12], готує таблиці і схеми в робочому зошиті, виводить робочі формули і формули для похибок вимірювань, складає програми розрахунків на ЕОМ.
Нижче приводимо основні вимоги до підготовки і оформлення звіту про лабораторну роботу.
1. Підготовка до лабораторної роботи. В робочому зошиті повинні бути записи (в довільній формі) по наступних пунктах:
- назва роботи;
- відповіді на теоретичні питання, знання яких необхідне для виконання роботи;
- опис експериментальної установки;
- робочі формули та їх вивід;
- формули для оцінки похибок вимірювань та їх вивід;
- таблиця для запису результатів вимірювань.
Всі розрахунки виконуються в робочому зошиті протягом лабораторного заняття.
2. Порядок допуску до виконання лабораторної роботи. До виконання роботи студент допускається, якщо він:
- вивчив явища, закони, які досліджуються чи застосовуються в даній лабораторній роботі;
- знає методику експерименту, хід виконання роботи;
- оформив звіт про лабораторну роботу, виконану на попередньому занятті;
- захистив всі виконані попередні роботи (має заборгованість не більше, ніж із двох робіт).
3. Оформлення звіту про виконану роботу. Звіт про лабораторну роботу виконується студентом в окремому зошиті протоколів лабораторних робіт після виконання роботи згідно наступної схеми:
- назва роботи;
- мета роботи;
- використані матеріали і прилади;
- короткі теоретичні відомості про явища, що вивчаються в роботі;
- схема установки і опис її роботи;
- хід виконання роботи;
- кінцевий результат вимірювань і оцінка похибок вимірювань;
- аналіз одержаних результатів і висновки.
ОСНОВИ ТЕОРІЇ ПОХИБОК
1.Вимірювання фізичних величин, обробка результатів вимірювання.
Основу науково-технічних знань становлять вимірювання. Про значення вимірювань дуже вдало висловився Д.І.Менделєєв: ”Наука починається… з того часу, коли починають вимірювати…”.Вимірювання мають важливе значення і у практичному житті людини. Завдяки вимірюванням кількісно характеризуються властивості фізичних об’єктів, мірою яких є фізична величина. Згідно державної системи стандартів: ”Фізична величина – це властивість, спільна в якісному відношенні для багатьох фізичних об’єктів (фізичних систем, їхніх станів та процесів, що в них відбуваються), але в кількісному відношенні – індивідуальна для кожного об’єкта”. “Вимірювання – знаходження значення фізичної величини дослідним шляхом за допомогою спеціальних технічних засобів”.
Технічні засоби, які використовуються для вимірювань і мають нормовані метрологічні властивості, називаються засобами вимірювання. Їх поділяють на міри (наприклад: міра маси – важок, гиря; міра довжини – лінійка, метр, мікрометр), вимірювальні перетворювачі, прилади (штангенциркуль, амперметр, тощо), вимірювальні установки (місток Уітстона).
Кожному фізичному об’єкту властиве певне значення фізичної величини. Значення, яке ідеально відтворює властивості даного об’єкта в кількісному та в якісному відношенні, називають істинним значенням фізичної величини. Істинні значення не залежать від засобів нашого пізнання і є тією абсолютною істиною, до якої ми прагнемо, намагаючись виразити їх у вигляді чисел. Істинне значення величини ми можемо оцінити експериментальним шляхом за допомогою засобів вимірювання. Значення величини, знайдене вимірюваннями, називають результатом вимірювання. Результат вимірювання - це продукт нашого пізнання, наближена оцінка істинного значення величини. Він залежить не лише від самого значення величини, яку оцінюють, але і від засобів вимірювання, методів вимірювання, від навичок і властивостей органів чуття експериментатора.
Величина, яка характеризує відхилення результату вимірювання від істинного значення вимірюваної величини є однією з найважливіших характеристик вимірювання і називається похибкою вимірювань.
Якщо х - результат вимірювання, а 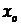 - істинне значення вимірюваної величини, то різниця між ними виражає так звану абсолютну похибку:
- істинне значення вимірюваної величини, то різниця між ними виражає так звану абсолютну похибку:
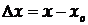 . (1)
. (1)
Всі вимірювання поділяються на такі види: прямі, посередні або непрямі, сукупні та спільні.
Прямі вимірювання: шукане значення величини знаходять безпосередньо з дослідних даних порівнянням з мірою цієї величини чи безпосередньо за відліковим пристроєм вимірювального приладу.
Посередні (непрямі) вимірювання - це такі вимірювання, результат яких знаходять на основі прямих вимірювань величин, пов’язаних з вимірюваною величиною відомою аналітичною, графічною чи табличною залежністю. Приклад: знаходження густини речовини r однорідного тіла за його масою m та геометричними розмірами; для тіла у формі прямокутного паралелепіпеда довжиною а, шириною в, висотою с:
r = m/(а×в×с)
Сукупні вимірювання - це такі, коли виконуються одночасно вимірювання кількох однойменних величин, за якими шукані значення величин знаходять розв’язуванням системи рівнянь, знайдених при прямих вимірюваннях різних комбінацій цих величин. Приклад: знаходження маси зважуванням. Нехай маємо гирі 1 кг, 2 кг і 5 кг, та деякі невідомі маси т 1 і т 2. Нехай зважування на терезах дало такий результат (рівновагу терезів): 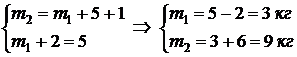 .
.
Спільні вимірювання - це такі, в результаті яких одночасно вимірюють кілька різнойменних величин для визначення залежності між ними. Приклад: залежність опору провідника від температури для знаходження, наприклад, температурних коефіцієнтів опору, струму від напруги для оцінки вольт-амперних характеристик діода. Одночасним вимірюванням сили струму у колі і падіння напруги на змінному опорі цього кола знаходять е.р.с. та внутрішній опір джерела струму: нехай при деяких двох значеннях змінного опору виміряні значення є 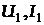 і
і  ; тоді
; тоді  .
.
У залежності від умов проведення експерименту вимірювання поділяють на рівноточні (умови при проведенні досліду залишаються незмінними) і нерівноточні.
2. Види похибок вимірювань.
Мета вимірювання-знаходження результату вимірювання (наближеної оцінки істинного значення фізичної величини) та оцінка його відхилення від істинного значення. Характеризує це відхилення абсолютна похибка, яка визначається формулою (1).
Оскільки х 0 (істинне значення) невідоме, то його замінюють дійсним значенням Х, яке знаходять на експерименті і яке найкраще наближається до істинного. Тоді похибку обчислюють за формулою:
 (2)
(2)
Найпростіше ця формула використовується в тих випадках, коли відоме Х. Наприклад, при встановленні похибок засобів вимірювання при їх перевірці (повірка засобів вимірювання). Якщо при повірці гирі, на якій нанесено 100 г, виявиться, що маса дорівнює 100,030 г, то 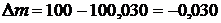 г. А дійсне значення маси гирі
г. А дійсне значення маси гирі 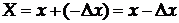 , оскільки поправка дорівнює похибці, взятій з протилежним знаком. Якщо похибку в -0,030 г матиме гиря масою 5 г, то зрозуміло, що гиря в 100 г виготовлена точніше. Для порівняння користуються так званою відносною похибкою, яка визначається за формулою
, оскільки поправка дорівнює похибці, взятій з протилежним знаком. Якщо похибку в -0,030 г матиме гиря масою 5 г, то зрозуміло, що гиря в 100 г виготовлена точніше. Для порівняння користуються так званою відносною похибкою, яка визначається за формулою
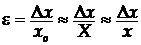 (3)
(3)
і виражається в процентах. Величина обернена до похибки називається точністю вимірювання. Якщо похибка вимірювання становить 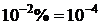 , то точність дорівнює
, то точність дорівнює 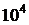 .
.
Оскільки істинне значення фізичної величини залишається невідомим, то похибку вимірювання точно встановити неможливо. Під час обробки результатів спостережень оцінюється лише проміжок, в якому може знаходитися значення похибки, а отже, й результат вимірювання матиме не одне, конкретне, значення, а множину значень.
Щоб оцінити похибки вимірювання, потрібно розглянути їх характер і причини появи. Щодо останніх похибки поділяються на три класи: випадкові, систематичні й промахи.
Випадкова похибка - складова похибки вимірювання, яка змінюється випадково під час повторних вимірювань однієї й тієї самої величини. Її наявність виявляється в тому, що при повторенні вимірювань тієї самої величини з однаковою ретельністю дістають значення, які відрізняються від попередніх останніми значущими цифрами. Випадкові похибки зумовлюються багатьма причинами, дія яких на результат кожного спостереження різна і не може бути врахована наперед (струси фундаменту будинку, вплив незначних переміщень повітря, тощо).
Систематична похибка - складова похибки вимірювання, яка залишається сталою або закономірно змінюється під час повторних вимірювань тієї самої величини. Вона завжди односторонньо впливає на результати спостережень, тільки збільшуючи, чи тільки зменшуючи їх. Наприклад, похибки мір, що виникають у результаті допусків під час їх виготовлення, похибки показів вимірювальних приладів через неточне їх градуювання і т.д. До систематичних похибок належить похибка внаслідок не абсолютної рівності плеч терезів.
Промахи - грубі похибки, які спотворюють результати вимірювань. Причинами їх виникнення можуть бути: неправильне визначення ціни поділки шкали (особливо, коли ціна поділки змінюється), помилковий відлік поділок шкали, помилковий запис результату спостереження (описка), пропуски в спостереженнях, помилки під час обчислення чи переписування. Як правило, результати таких вимірювань вилучаються з сукупності даних вимірювань.
3. Похибки прямих вимірювань [2,3]
Нехай у результаті повторюваних рівноточних вимірювань фізичної величини маємо послідовність значень:
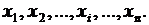
Подамо результати n вимірювань у вигляді:
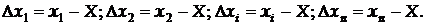 (4)
(4)
Підсумовуючи члени в (4), дістаємо:
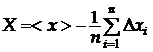 де
де 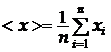
– середнє арифметичне значення вимірюваної величини.
При великій кількості вимірювань, у випадку їх нормального (гаусівського) розподілу, випадкові відхилення 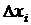 , однакові за модулями, але з різними знаками, зустрічаються однаково часто, тому
, однакові за модулями, але з різними знаками, зустрічаються однаково часто, тому
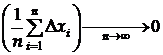 , а
, а 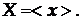
Отже, при 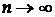 істинне значення фізичної величини дорівнює середньому арифметичному (звичайно, якщо при цьому немає систематичних похибок).
істинне значення фізичної величини дорівнює середньому арифметичному (звичайно, якщо при цьому немає систематичних похибок).
У реальній метрологічній практиці число вимірювань n є скінченою величиною. Через це завдання теорії обробки результатів вимірювань зводиться до оцінки ступеня наближення вимірюваного значення до істинного.
Прояв випадкової події визначається імовірністю Р. Імовірністю називається число, навколо якого групуються відносні частоти появи випадкової події в різних серіях випробувань.
Відносною частотою події А (РА) називається відношення числа появи певної події n A до числа всіх випробувань n 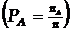 .
.
Повне описання появи випадкових подій здійснюється за допомогою функції розподілу ймовірностей. Аналогічно використовується і функція розподілу випадкових похибок.
Інтегральною функцією розподілу, або просто функцією розподілу випадкової величини 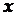 , називається функція F (
, називається функція F (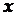 ), яка дорівнює ймовірності того, що випадкова величина
), яка дорівнює ймовірності того, що випадкова величина 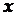 набуває значення, яке менше від деякого числа
набуває значення, яке менше від деякого числа 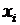 , тобто
, тобто 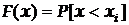 .
.
Геометричний зміст функції розподілу полягає в тому, що при кожному значенні x функція F (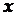 ) дорівнює ймовірності того, що випадкова величина x набуває на числовій осі значень, які містяться ліворуч від точки x.
) дорівнює ймовірності того, що випадкова величина x набуває на числовій осі значень, які містяться ліворуч від точки x.
У теорії ймовірностей стосовно до фізичних вимірювань розглядаються випадкові величини, можливі значення яких містяться в певному інтервалі 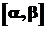 .
.
На основі закону розподілу ймовірностей такої випадкової величини x визначається імовірність попадання її значення в довільний інтервал 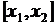 , який міститься всередині
, який міститься всередині 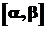 . Цю імовірність позначатимемо
. Цю імовірність позначатимемо 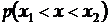 . Обмежимося тільки такими випадковими величинами x, для яких імовірність попадання в інтервал
. Обмежимося тільки такими випадковими величинами x, для яких імовірність попадання в інтервал 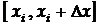 малої довжини
малої довжини 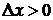 можна вважати пропорційною довжині цього інтервалу:
можна вважати пропорційною довжині цього інтервалу:
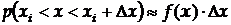
Точний зміст цього співвідношення дається граничним співвідношенням
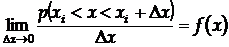 ,
,
де функція 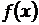 називається густиною розподілу випадкової величини
називається густиною розподілу випадкової величини 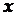 ,а добуток
,а добуток 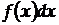 - елементом імовірності. Користуючись елементом імовірності, шляхом інтегрування можна знайти імовірність попадання значення
- елементом імовірності. Користуючись елементом імовірності, шляхом інтегрування можна знайти імовірність попадання значення 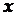 в довільний інтервал
в довільний інтервал 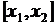 :
:
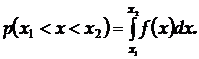 (5)
(5)
Густина розподілу має такі властивості:
1) 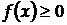 , як похідна неспадної функції p (x), що пов’язано з невід’ємністю ймовірностей;
, як похідна неспадної функції p (x), що пов’язано з невід’ємністю ймовірностей;
2) функція повинна бути нормована:
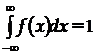 , (6)
, (6)
яка відображає вірогідність події 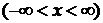 . Якщо всі можливі значення випадкової величини
. Якщо всі можливі значення випадкової величини 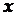 скупчені в скінченому інтервалі
скупчені в скінченому інтервалі 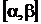 (отже, поза цим інтервалом
(отже, поза цим інтервалом 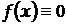 ), то умова (6) набирає вигляду:
), то умова (6) набирає вигляду:
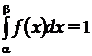 .
.
З (5) випливає, що імовірність попадання випадкової величини 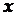 в інтервал
в інтервал 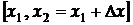 геометрично можна подати площею криволінійної трапеції, обмеженої графіком функції розподілу, ординатами
геометрично можна подати площею криволінійної трапеції, обмеженої графіком функції розподілу, ординатами 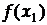 і
і 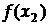 (на осі ординат відкладається значення
(на осі ординат відкладається значення 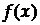 ) та віссю абсцис.
) та віссю абсцис.
Підкреслимо, що густина розподілу ймовірностей, знайдена вище, визначає закон розподілу неперервної величини 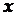 . Густину розподілу
. Густину розподілу 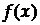 називають ще диференціальною функцією розподілу.
називають ще диференціальною функцією розподілу.
Досвід обробки результатів вимірювань показує, що розподіл похибок описується різними законами. Проте досить часто для опису розподілу випадкових похибок використовується нормальний закон розподілу (закон Гауса)
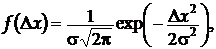 D x = x - x o (7)
D x = x - x o (7)
де 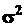 - дисперсія генеральної сукупності, а
- дисперсія генеральної сукупності, а 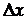 - відхилення від істинного значення. Генеральною сукупністю називається множина всіх можливих значень вимірювань
- відхилення від істинного значення. Генеральною сукупністю називається множина всіх можливих значень вимірювань 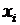 або можливих значень похибок
або можливих значень похибок 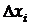 .
.
Закон Гауса знаходить широке застосування в теорії похибок. Це зумовлене такими причинами:
1) для великої кількості вимірювань рівні за модулем, але протилежні за знаком, похибки зустрічаються однаково часто;
2) малі за модулем похибки зустрічаються частіше, ніж великі, тобто імовірність появи похибки тим менша, чим більше її абсолютне значення;
3) похибки вимірювань становлять неперервний ряд значень.
На рис. 1 наведено форму кривої розподілу Гауса для трьох значень 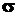 . Початок координат розміщено в точці з нульовою похибкою. Для нормального закону розподілу є характерним
. Початок координат розміщено в точці з нульовою похибкою. Для нормального закону розподілу є характерним  його симетрія (при великій кількості вимірювань появи випадкових похибок, які рівні за величиною, але різні за знаком - рівноімовірні) і монотонність зменшення густини ймовірності (поява великих випадкових похибок - малоімовірна). Права і ліва вітки кривої Гауса асимптотично наближаються до осі абсцис.
його симетрія (при великій кількості вимірювань появи випадкових похибок, які рівні за величиною, але різні за знаком - рівноімовірні) і монотонність зменшення густини ймовірності (поява великих випадкових похибок - малоімовірна). Права і ліва вітки кривої Гауса асимптотично наближаються до осі абсцис.
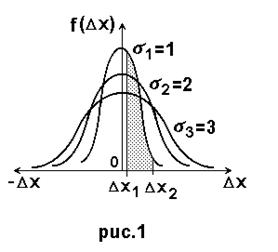
Закон Гауса - одномодальний. Максимальне значення закону розподілу (густини імовірності) називається модою. Закон розподілу з одним максимальним значенням називається одномодальним, з двома- двомодальним і т.д. Мода нормального розподілу дорівнює 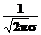 . Чим менше
. Чим менше 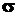 , тим вище, гостріше крива розподілу і навпаки. Із збільшенням
, тим вище, гостріше крива розподілу і навпаки. Із збільшенням 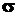 зростає розкид відліків, тобто точність вимірювання зменшується. Величина
зростає розкид відліків, тобто точність вимірювання зменшується. Величина 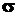 - є основним параметром, який визначає вид кривої розподілу випадкових похибок.
- є основним параметром, який визначає вид кривої розподілу випадкових похибок.
Зміст функції Гауса такий. Площа фігури, обмеженої кривою Гауса, віссю 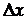 і лініями -
і лініями - 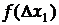 і
і 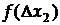 (заштрихована площа на рис.1), чисельно дорівнює імовірності, з якою довільний відлік попадає в інтервал
(заштрихована площа на рис.1), чисельно дорівнює імовірності, з якою довільний відлік попадає в інтервал 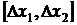 .
.
Безпосереднім інтегруванням (5) можна пересвідчитися, що вся площа під кривою Гауса дорівнює точно одиниці.
Для оцінки величини випадкової похибки є кілька способів. Найбільш поширеною є оцінка за допомогою середньої квадратичної (або стандартної) похибки 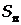 , згідно з означенням:
, згідно з означенням:
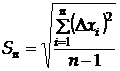 . (8)
. (8)
Генеральна сукупність (всі можливі значення вимірювальної величини при 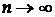 ) характеризується математичним сподіванням або генеральним середнім -
) характеризується математичним сподіванням або генеральним середнім - 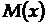 і дисперсією -
і дисперсією - 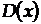 .
.
Центр розкиду значень 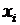 відповідає математичному сподіванню
відповідає математичному сподіванню 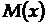 , яке являє собою істинне значення вимірюваної величини. Дисперсія - це міра відхилення випадкових величин від математичного сподівання: чим більше
, яке являє собою істинне значення вимірюваної величини. Дисперсія - це міра відхилення випадкових величин від математичного сподівання: чим більше 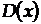 , тим менш точні вимірювання.
, тим менш точні вимірювання.
Для нормального розподілу випадкових величин
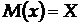 ;
; 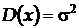 .
.
Мірою розсіяння вимірюваних значень 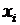 відносно
відносно 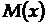 є також середнє квадратичне (або стандартне) відхилення:
є також середнє квадратичне (або стандартне) відхилення: 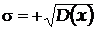 .
.
В лабораторній практиці вимірювань дістають обмежене число виміряних значень величини і тому обчислюють лише наближені значення 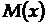 і
і 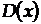 ; їх називають оцінками.
; їх називають оцінками.
Оцінкою математичного сподівання є середнє арифметичне виміряних даних фізичної величини
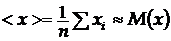 ,
, 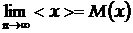 . (9)
. (9)
Оцінками дисперсії D та стандартного відхилення s є
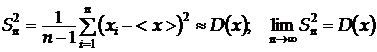 ;
;
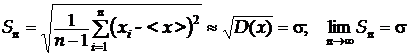 .
.
Зауважимо, що результат вимірювання величин 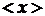 , обчислений за (9), є також випадковою величиною (про це ми переконаємося при виконанні лабораторної роботи №1).
, обчислений за (9), є також випадковою величиною (про це ми переконаємося при виконанні лабораторної роботи №1).
Для оцінки точності результату виміряного значення фізичної величини використовують такі характеристики: надійний інтервал та граничну похибку середнього арифметичного.
Надійний (або довірчий) інтервал - це інтервал, який містить істинне значення X виміряної фізичної величини 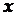 із заданою імовірністю
із заданою імовірністю  , яка називається надійною (або довірчою) імовірністю (або коефіцієнтом надійності). При цьому справедливий вираз
, яка називається надійною (або довірчою) імовірністю (або коефіцієнтом надійності). При цьому справедливий вираз
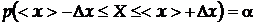 , (10)
, (10)
де 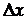 – гранична похибка
– гранична похибка 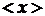 , яка дорівнює половині надійного інтервалу (10),
, яка дорівнює половині надійного інтервалу (10),
 , (11)
, (11)
де 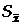 – оцінка стандартного відхилення
– оцінка стандартного відхилення 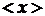 від істинного значення Х (середня квадратична похибка середнього арифметичного), яка обчислюється за формулою
від істинного значення Х (середня квадратична похибка середнього арифметичного), яка обчислюється за формулою
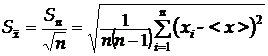 ;
;
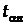 – нормований коефіцієнт Стьюдента (табл.1, Додаток); n – число ступенів вільності (для знаходження коефіцієнта Стьюдента
– нормований коефіцієнт Стьюдента (табл.1, Додаток); n – число ступенів вільності (для знаходження коефіцієнта Стьюдента 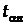 число ступенів вільності беруть таким, що дорівнює n-1при обробці однієї групи вимірювань, розподілених за нормальним законом для невеликих вибірок з генеральної сукупності (вибірка – скінчене число значень величини
число ступенів вільності беруть таким, що дорівнює n-1при обробці однієї групи вимірювань, розподілених за нормальним законом для невеликих вибірок з генеральної сукупності (вибірка – скінчене число значень величини 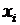 ). Результати вимірювань записуються у вигляді
). Результати вимірювань записуються у вигляді
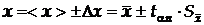 .
.
Отже, коефіцієнт Стьюдента залежить від надійної імовірності та кількості вимірювань.
Якщо надійний інтервал збільшується, то зростає імовірність того, що істинне значення величини попаде в розглядуваний інтервал. Високий ступінь надійності необхідний при відповідальних вимірюваннях. Надійну імовірність  прийнято задавати такою, що дорівнює 0,90; 0,95; 0,98; 0,99 (значення 0,99 рекомендується брати для випадків, коли вимірювання не можна повторити; в особливо відповідальних випадках, коли результати вимірювання мають певне значення для здоров’я людей, допускається брати більш високу надійну імовірність).
прийнято задавати такою, що дорівнює 0,90; 0,95; 0,98; 0,99 (значення 0,99 рекомендується брати для випадків, коли вимірювання не можна повторити; в особливо відповідальних випадках, коли результати вимірювання мають певне значення для здоров’я людей, допускається брати більш високу надійну імовірність).
Отже, для характеристики величини випадкової похибки потрібне знання двох чисел: значення самої похибки (або надійного інтервалу D х) та значення надійної імовірності a.
Використання середньої квадратичної похибки як основного числового виразу випадкової похибки є зручним на тій підставі, що цій величині відповідає цілком певна надійна імовірність, яка дорівнює 0,68; подвоєній середній квадратичній похибці 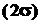 відповідає надійна імовірність -0,95, потроєній -
відповідає надійна імовірність -0,95, потроєній -  -0,999.
-0,999.
Розподіл Стьюдента справедливий для малого числа вимірювань (n³2), що і характерно як для техніки, так і для наукових досліджень. Із зростанням числа вимірювань розподіл Стьюдента прагне до нормального розподілу (фактично при n>20). Математичного виразу розподілу Стьюдента ми не наводимо, зважаючи на його складність.
Характерним для розподілу Стьюдента є його незалежність від параметрів 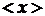 (або
(або 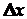 ) та s нормальної генеральної сукупності, а також можливість оцінки при невеликому числі вимірювань (n<20) похибки
) та s нормальної генеральної сукупності, а також можливість оцінки при невеликому числі вимірювань (n<20) похибки 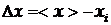 за заданою надійною імовірністю a або знаходженням надійності вимірювань за заданим значенням
за заданою надійною імовірністю a або знаходженням надійності вимірювань за заданим значенням 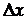 .
.
Розподіл Стьюдента дає також змогу встановити, що при досить великому n середнє арифметичне значення 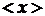 з імовірністю, близькою до вірогідності, дуже мало відрізняється від істинного значення х o.
з імовірністю, близькою до вірогідності, дуже мало відрізняється від істинного значення х o.
Методика визначення та єдиний підхід до оцінки показників точності вимірювань для основних видів вимірювання знайшли своє відображення в ГОСТ 8000-72 (Державна система забезпечення єдності вимірювань. Основні положення) та в спеціальних метрологічних працях.
Статистична обробка результатів прямих вимірювань з багаторазовими спостереженнями виконується згідно схеми №1.
Схема №1 обробки результатів прямих вимірювань [3].
Необхідно враховувати як випадкові, так і систематичні похибки і починати із виключення відомих систематичних похибок і визначення невиключених систематичних похибок, зокрема інструментальних.
Для знаходження випадкової похибки треба виконати кілька спостережень в такій послідовності:
1.Вимірюють фізичну величину n разів і дані заносять в таблицю.
2.Відкидають промахи.
3.Знаходять середнє значення шуканої величини 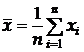 .
.
4.Обчислюють похибки кожного із вимірів 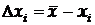 .
.
5.Обчислюють квадрати похибок 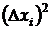 .
. 
6.Визначають середню квадратичну похибку середнього арифметичного
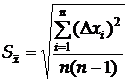 .
.
7.Задають значення коефіцієнта надійності (надійної імовірності)  (0,95 або 0,9).
(0,95 або 0,9).
8.Знаходять за таблицею №1 (Додаток) для вибраного n і заданого  коефіцієнт Стьюдента
коефіцієнт Стьюдента 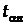 .
.
9.Визначають межі надійного інтервалу 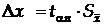 .
.
10.Якщо величина D х (межа надійного інтервалу) виявиться порівняною з величиною систематичної похибки (інструментальної похибки), то за межу надійного інтервалу слід взяти результуючу похибку
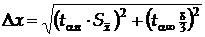 ,
,
де 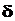 - величина похибки приладу, а
- величина похибки приладу, а  – коефіцієнт Стьюдента при n=¥. Систематична похибка вимірювання може бути визначена за формулою
– коефіцієнт Стьюдента при n=¥. Систематична похибка вимірювання може бути визначена за формулою 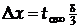 , або ж оцінюється як половина ціни поділки вимірного приладу.
, або ж оцінюється як половина ціни поділки вимірного приладу.
11.Обчислюють відносну похибку результату серії вимірювань 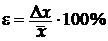 .
.
12.Кінцевий результат записують у вигляді  .
.
4. Похибки посередніх (непрямих) вимірювань [3].
а) Метод дисперсій.
Нехай вимірювана величина y є функцією кількох величин 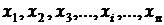 , значення яких знаходять прямими вимірюваннями. Ці величини є аргументами. Отже можемо записати:
, значення яких знаходять прямими вимірюваннями. Ці величини є аргументами. Отже можемо записати:
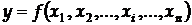 .
.
Значення 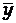 знаходять за середніми арифметичними значеннями аргументів:
знаходять за середніми арифметичними значеннями аргументів:
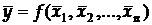 . (12)
. (12)
Зупинимося на найпростішому випадку, коли  .
.
Абсолютна похибка прямого вимірювання величини x дорівнює 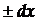 і нею зумовлена похибка функції
і нею зумовлена похибка функції 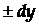 . Очевидно, що
. Очевидно, що
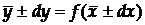 . (13)
. (13)
Розкладемо праву частину (13) в ряд Тейлора:
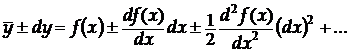
Обмежуючись членами, які містять першу степінь, одержимо:
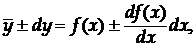
тоді
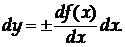
Оскільки вимірювана нами величина в загальному задається формулою (12), то при однаковому коефіцієнті надійності a для цих прямих вимірювань надійна межа похибки посереднього вимірювання знаходиться за формулою:
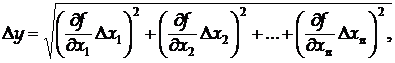 (15)
(15)
де 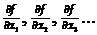 - частинні похідні y по
- частинні похідні y по 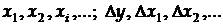 - надійні межі похибок вимірювання величин
- надійні межі похибок вимірювання величин 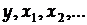 .
.
Межа відносної похибки дорівнює:
 . (16)
. (16)
Значення похідних обчислюють при 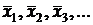 .
.
Застосувавши ці формули для функцій певного виду, відповідно знайдемо похибки за формулами, приведеними в таблиці №3 [2].
б) Метод приведення.
У посередніх вимірюваннях можна значення функції обчислювати для кожного окремого спостереження
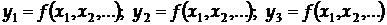 ,
,
а надійну межу похибки посереднього вимірювання – в результаті обробки вибірки 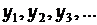 як це робимо в прямих вимірюваннях, наприклад:
як це робимо в прямих вимірюваннях, наприклад:
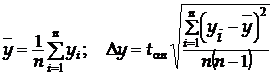 і т.д.
і т.д.
Щоб знайти результат посереднього вимірювання, виконують математичні операції, і результати обчислень округлюють. Тому, очевидно, немає потреби виконувати обчислення з результатами прямих вимірювань як з точними числами, а робити їх, знайшовши необхідну кількість значущих цифр у результаті. Це значно полегшить обчислення і звільнить від зайвої роботи, але в таких обчисленнях неминучі похибки. Щоб можна було нехтувати похибкою заокруглення при обчисленнях, вона повинна бути хоча б у 10 раз менша за похибку посередніх вимірювань. Тому всі обчислення слід проводити з такою кількістю значущих цифр, які перевищують на одиницю кількість значущих цифр, знайдених при вимірюваннях (для наступного округлення результату). Похибка однозначного числа не менша від 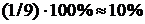 , двозначного –
, двозначного – 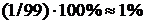 , тризначного –
, тризначного – 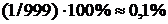 . Тому при обчисленнях потрібно додержувати таких правил:
. Тому при обчисленнях потрібно додержувати таких правил:
а) якщо відносна похибка результату вимірювань становить 10-100%, обчислення можна виконувати з двома значущими цифрами;
б) якщо відносна похибка 1-10%, обчислення можна виконувати з трьома значущими цифрами (ще можна використовувати логарифмічну лінійку);
в) якщо відносна похибка 0,1-1%, обчислення можна виконувати з чотирма значущими цифрами (наприклад, за допомогою чотиризначних таблиць) і т.д.
У обчисленнях доводиться користуватися наближеними значеннями чисел, наприклад 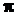 . Округлюючи число (тобто замінюючи його наближеним значенням) до різних розрядів, дістанемо різні за значенням і знаком похибки. Щоб нехтувати похибкою таких чисел під час обчислення результату вимірювань, треба брати їх з такою кількістю значущих цифр, щоб похибка округлення була на порядок менша за похибку результату вимірювання.
. Округлюючи число (тобто замінюючи його наближеним значенням) до різних розрядів, дістанемо різні за значенням і знаком похибки. Щоб нехтувати похибкою таких чисел під час обчислення результату вимірювань, треба брати їх з такою кількістю значущих цифр, щоб похибка округлення була на порядок менша за похибку результату вимірювання.
Так само слід підходити до табличних і експериментальних даних. Якщо табличні дані наводяться без похибок, вважається, що похибка даного значення є похибкою округлення і межа її дорівнює 0,5 одиниці розряду останньої цифри числа. Похибка округлення підлягає рівномірному розподілу. Тому, коли треба визначити надійну межу похибки даного значення з довірчою імовірністю a, використовують формулу:
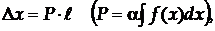 (18)
(18)
в якій 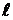 дорівнює 0,5 одиниці розряду останньої цифри числа.
дорівнює 0,5 одиниці розряду останньої цифри числа.
Результати сукупних вимірювань і надійні інтервали їх похибок можна знайти методами обробки результатів посередніх вимірювань, згідно схеми №4 [3].
СХЕМА №4
1. Для кожної вибірки величин прямих вимірів, які входять в ролі аргументу в досліджувану функцію, проводиться обробка результатів за схемою №1 для прямих вимірювань при одному і тому ж значенні коефіцієнта надійності  .
.
2. Вираховують середнє значення шуканої величини
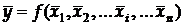
3. Оцінюють межі надійного інтервалу для результату непрямих вимірювань
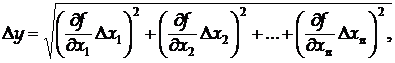
де похідні 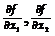 і т.д. вираховуються при середніх значеннях аргументів
і т.д. вираховуються при середніх значеннях аргументів  і т.д.
і т.д.
4. Визначають відносну похибку 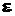 :
:
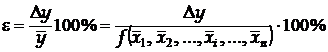 .
.
5. Кінцевий результат записують у формі:
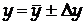
5. Графічне представлення результатів спільних вимірювань
Результати спільних вимірювань часто зображують графічно. Перевага графічного зображення в тому, що воно дає наочне зображення досліджуваної залежності між фізичними величинами, дає змогу швидко визначити деякі значення (наприклад, максимальне значення функції).
Похибку в експериментальному значенні на графіку можна вказувати рисками інтервалів:  . Оскільки нанесення таких значків вимагає додаткових затрат часу і призводить до ускладнення графіків, їх треба наносити лише тоді, коли потрібні. Доцільність нанесення похибок на графіку можна продемонструвати на такому прикладі. Нехай потрібно провести криву через експериментальні точки, зображені на рис.2. З’єднати точки графіка ламаною лінією (а) не можна, бо це означало б, що при зміні однієї величини друга змінюється стрибками, що мало ймовірно. Як саме з’єднати точки, яку саме криву провести – пряму лінію чи плавну криву – визначають межі похибок вимірювань. Якщо вони такі як на графіку “б”, то через точки графіка треба провести плавну криву; якщо ж похибки такі, як на графіку “в”, то слід провести пряму лінію, бо вона є найпростішою функціональною залежністю. Експериментальні значення задовольняють і рівняння кривої графіка “б”, але при таких великих похибках через експериментальні точки можна провести багато різних кривих, що відповідатимуть великій кількості функціональних залежностей. Тому через експериментальні точки, що на рис.2в, найкраще провести пряму лінію.
. Оскільки нанесення таких значків вимагає додаткових затрат часу і призводить до ускладнення графіків, їх треба наносити лише тоді, коли потрібні. Доцільність нанесення похибок на графіку можна продемонструвати на такому прикладі. Нехай потрібно провести криву через експериментальні точки, зображені на рис.2. З’єднати точки графіка ламаною лінією (а) не можна, бо це означало б, що при зміні однієї величини друга змінюється стрибками, що мало ймовірно. Як саме з’єднати точки, яку саме криву провести – пряму лінію чи плавну криву – визначають межі похибок вимірювань. Якщо вони такі як на графіку “б”, то через точки графіка треба провести плавну криву; якщо ж похибки такі, як на графіку “в”, то слід провести пряму лінію, бо вона є найпростішою функціональною залежністю. Експериментальні значення задовольняють і рівняння кривої графіка “б”, але при таких великих похибках через експериментальні точки можна провести багато різних кривих, що відповідатимуть великій кількості функціональних залежностей. Тому через експериментальні точки, що на рис.2в, найкраще провести пряму лінію.
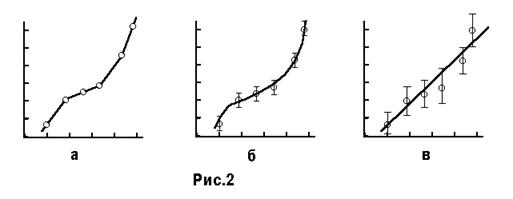
Графіки часто використовують для того, щоб перевірити, чи задовольняє досліджувана залежність ту або іншу функцію. При цьому лінію проводять між експериментальними точками так, щоб вони розташовувались, по можливості, в однаковій кількості по обидві сторіни лінії. Детально про графічну обробку експериментальних даних описано в методичному посібнику [2], стор.103-132, та [3].
6. Похибки заокруглення
Часто табличні значення математичних або фізичних постійних, а також розраховані результати непрямих вимірювань і їх похибок, у записі кінцевого результату необхідно представляти наближеним числом з певною кількістю значущих цифр. Значущими цифрами довільного числа називаються всі правильні і перша сумнівна цифри 1, 2, 3,... 9, що входять у число, а також 0 (нуль, якщо він стоїть всередині або справа). Тому при заокругленні результату вимірювання узвичай залишають тільки значущі цифри, тобто всі правильні і одну сумнівну цифри.
Деяка k-та цифра наближеного числа правильна, якщо абсолютна похибка D х не перевищує половини одиниці k-го розряду. Наприклад, якщо це розряд одиниць – то при D х £0,5; якщо це розряд десяткових – то при D х £0,05 і т.д., тобто цифра, наприклад, в розряді десяткових є останньою правильною цифрою, якщо похибка D х £0,05, а наступна цифра в розряді сотих є вже першою сумнівною. У противному випадку цифру k-го розряду називають першою сумнівною цифрою (тобто при D х >0,5×10k). Таким чином, величина похибки визначає місцеположення (розряд) правильних і сумнівних цифр у наближеному числі, яке отримане в результаті вимірювання, і при його заокругленні залишають всі правильні і тільки одну (першу) сумнівну цифри. У свою чергу це накладає обмеження на вибір кількості цифр при запису значення похибки D х і яке визначається такими двома правилами. Число вимірювань 3<n<10: при запису значення D х необхідно зберегти дві значущі цифри, якщо перша 1 або 2, і достатньо записати одну значущу цифру, якщо перша 3 і більше (відносна похибка заокруглення до числа 3 становить»17%, тоді як така ж похибка оцінки самого СКВ Sn або 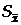 становить»24% [3]). Число вимірювань n>10: при запису значення D х необхідно зберегти дві значущі цифри, якщо перша 1, 2 або 3 і достатньо записати одну значущу цифру, якщо перша 4 і більше.
становить»24% [3]). Число вимірювань n>10: при запису значення D х необхідно зберегти дві значущі цифри, якщо перша 1, 2 або 3 і достатньо записати одну значущу цифру, якщо перша 4 і більше.
Для задоволення цього способу запису кількості цифр у числі проводять його заокруглення. Нехай після заокруглення в числі повинно залишитись k значущих чисел, тоді користуються такими правилами:
- якщо k+1 цифра менше 5, то цифра k не змінюється;
- якщо k+1 цифра більше 5, то цифра k збільшується на 1;
- якщо k+1 цифра дорівнює 5, то можливі два випадки:
а) якщо серед цифр, що відкидаються, крім цифри 5 є відмінні від 0, то k-та цифра збільшується на 1,
б) але якщо ці цифри 0, то: k-ту цифру збільшують на 1, якщо вона непарна, і залишають без змін, якщо вона парна (цифра 0 вважається парною).
Якщо з наближеними числами ще будуть проводитись обчислення, то в них необхідно зберігати не більше двох сумнівних цифр.
Виконуючи математичні операції з наближеними числами, необхідно дотримуватися правила: після виконання математичних операцій в кінцевому результаті необхідно залишити стільки значущих цифр після коми, скільки їх було в числі з найменшою кількістю таких цифр.
Приклад. При вимірюванні деяких 3-х одноіменних фізичних величин було проведено по 15 дослідів (вимірювань) і зроблені такі записи усереднених результатів і їх похибок: Х 1=3,405; Х 2=4,9784; Х 3=1,33175; D х 1=0,04159; D х 2=0,00553; D х 3=0,000359. Написати правильно результати вимірювань, а також суми і добутки одержаних величин.
Розв’язок. Враховуючи кількість зроблених вимірювань (15), дані похибки необхідно заокруглити, залишивши доцільну кількість значущих цифр:
D х 1=0,04159 – потрібно записати: D х 1=0,04;
D х 2=0,00553 – потрібно записати: D х 2=0,006;
D х 3=0,000359 – потрібно записати: D х 3=0,0036.
Після цього середні величини Хі також необхідно заокруглити, залишивши правильні і одну сумнівну цифри:
Х 1=3,40 – оскільки цифра 4 правильна (D х 1=0,04<0,05), тому залишається ще одна сумнівна цифра 0 (яка не збільшується на 1, бо є парною);
Х 2=4,98 – оскільки D х 2=0,06>0,05, то цифра сотих в числі Х 2 (7) вже є сумнівною, тому вона залишається, збільшуючись на 1, а інші відкидаються;
Х 3=1,3318 – цифри 1,3,3,1 – правильні (D х 3=0,00036<0,0005), 8 – сумнівна (7 непарна і при заокругленні збільшується на 1).
 =3,40+4,98+1,3318 = 9,7098 = 9,71;
=3,40+4,98+1,3318 = 9,7098 = 9,71;
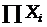 =3,40×4,98×1,3318 = 22,54098136 = 22,54 – результат математичної дії в даному прикладі заокруглюється до двох значущих цифр після коми (в числі Х 1 дві цифри після коми).
=3,40×4,98×1,3318 = 22,54098136 = 22,54 – результат математичної дії в даному прикладі заокруглюється до двох значущих цифр після коми (в числі Х 1 дві цифри після коми).
Лабораторна робота №1
 2018-02-13
2018-02-13 1556
1556







