VI. Порядок виконання роботи

1. Ввімкнути генератор і частотомір за 20 хвилин до початку роботи (вмикається лаборантом).

2. За допомогою частотоміра і секундоміра зробити n=50 відліків числа імпульсів 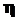, які поступили на вхід приладу за 10 секунд (частота генератора в діапазоні 25-100 Гц встановлюється керівником заняття). Результати вимірювань занести в таблицю 1.1.

Таблиця 1.1.

№ п/п	hi	ni, c-1	Dni,c-1	(Dni)2	№ п/п	hi	ni, c-1	Dni,c-1	(Dni)2	, с-1			Dn	a	t a
1					26
2					27
3					28
4					29
5					30
6					31
7					32
8					33
9					34
10					35
11					36
12					37
13					38
14					39
15					40
16					41
17					42
18					43
19					44
20					45
21					46
22					47
23					48
24					49
25					50

3. Вираховують з точністю до 0.1 для кожного відліку  - число імпульсів за 1 с, а також середнє значення , дисперсію  та середню квадратичну похибку середнього арифметичного  за формулами (1.8), (1.9), (1.10) і межі надійного інтервалу Dν для коефіцієнта надійності a=0.95, користуючись таблицею 1 (Додаток). Обчислення повторити за програмою №1 (Додаток).

4. Для визначення вигляду розподілу розбивають весь діапазон із значень n на інтервали Dν₀ (в даній роботі Dν₀=0,5 с^-1) і підраховують, яка кількість D n значень попадає в кожен інтервал. Обчислюють відносну частоту, яка приходиться на одиничний інтервал. Для цього складають таблицю 1.2.

5. Побудувати на міліметровому папері діаграму розподілу р _і в залежності від n, відклавши по осі абсцис значення (початки інтервалів), а по осі ординат h (див. табл.1.2). Діаграма буде представляти собою систему прямокутників, висоти яких , а основа - Dν₀.

6. На тому ж графіку в тому ж самому масштабі побудувати криву густини імовірності за формулою (1.7), замінивши m та s² їх наближеними значеннями  та . Для обчислень використовують програмовані калькулятори.

7. Вирахувати середні значення, середні квадратичні похибки і межі надійних (довірчих) інтервалів Dν для a=0,95 кожних п’яти значень. Скористатися програмованими калькуляторами.

8. Нанести на графік для порівняння всі середні значення і надійні інтервали для п’яти значень, зберігаючи масштаб, який був вибраний при побудові гістограми.

9. Оформлені результати повинні бути представлені у вигляді, даному на рис.1.2.

10. Зробити висновки.

Взірець таблиці 1.2.

Частота від-до, Гц	Кількість значень в інтервалі (риски)	D ni
47-47.5	///	3
47.51-48	/////	5
48.01-48.5	///////	6

     Примітка: На основі результатів нижньої частини рис.1.2 викладач акцентує увагу студентів, що для окремих вибірок одержані значення вимірюваних величин з відповідними довірчими інтервалами можуть не перекриватись. А це означає, що середнє значення вимірюваної величини окремої вибірки є також випадкова величина, яка може значно відрізнятися від середнього значення для великої вибірки.

Лабораторна робота №2