Теорема Н. Е. Жуковского

Пусть в точке С звена (АВ) (рис.3.10. а) приложена сила,  - угол между направлением движения точки С   и линией действия силы. Работа и мощность этой силы на элементарном перемещении точки ее приложения соответственно:

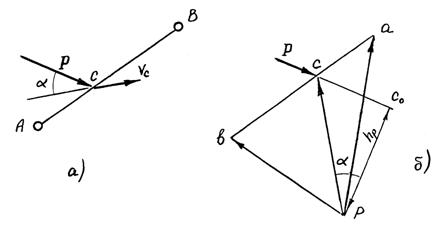
Рисунок 3.10 - К выводу теоремы Н.Е. Жуковского

Перенесем силу Р в одноименную точку повернутого на 90^о плана скорости (рис.3.10.б) звена. Рассматривая этот план скорости как жесткий рычаг, напишем момент силы Р относительно полюса:

где h_p - плечо силы P относительно p.

Из , тогда

Умножив обе части этого выражения на , получим:

или

Таким образом доказана теорема Н.Е. Жуковского: мощность силы, действующей на звено, пропорциональна моменту этой силы, приложенной в одноименной точке повернутого на 90^о плана его скорости, относительно полюса.

ОПРЕДЕЛЕНИЕ УРАВНОВЕШИВАЮЩЕЙ СИЛЫ С ПОМОЩЬЮ ТЕОРЕМЫ Н.Е. ЖУКОВСКОГО.

Пусть на звенья механизма действуют силы и момент (включая и инерции)

Если в эту систему включить и уравновешивающую силу, то из условия сохранения движения – динамического равновесия вытекает:

где dS_i - элементарные перемещения точек приложения сил,

 - угловые перемещения звена,

 - угол между P_i и dS_i

Заменив M_i парами сил, упростим

Разделив обе части на dt, получим:

Разделив обе части на  плана скоростей, имеем

где h_i - плечи сил P_i перенесенных в одноименные точки повернутого на 90^о плана скорости механизма.

Таким образом, для определения уравновешивающей силы с помощью рычага Н.Е. Жуковского следует:

1. построить повернутый на 90^о план скорости механизма,

2. определить на этом плане точки, одноименные точкам приложения сил на звенья,

3. приложить в этих точках соответствующие силы без изменения их направления, в том числе уравновешивающую силу,

4. рассматривая план скоростей как жесткий рычаг, из условия найти неизвестную уравновешивающую силу.