2018-03-09
247
1. Отсоединяем ведущее звено от механизма (рис. 3.11. ж):
2. В точку А приложим силу Рур ^ (ОА) и реакцию 
çê 
противоположную сторону направления и равной по величине (
) (рис. 3.11. ж);
3. Вычисляем 
, где (ОА), h – измеряется из чертежа в мм
Рычаг Жуковского
1. Построим повёрнутый на 90о план скорости механизма (рис. 3.11. з);
2. На этом плане определяем точки, одноимённые точкам, в которых на кинематической схеме к звеньям приложены силы, используя свойства плана скоростей из пропорции:
, 
В одноименные точки перенесем силы: G3, 
, P,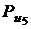 
, G5 и уравновешивающую силу Рур приложим в точке а 1^(ра 1) (рис. 3.11. з).
3. Составим условие равновесия рычага Н.Е. Жуковского
,
где значения h, h 1, (pс 5), (pа 1) берем из чертежа (рис. 3.11. з)
4. Достоверность расчетов Рур можно оценить отношением разности результатов из п. 8 и 9 к их среднеарифметической величине:
Пример2: Известный массы звеньев m5=13 кг m4=10 кг, m3=15 кг, m2=8 кг сила полезного сопротивления Рпс=15000 Н, моменты инерции звеньев, относительно оси проходящий через центр тяжести JS2 =0,03 кг м2, JS3= =0,075 кг м2, JS4 =0,03 кг м2.
1. Определить силы инерции звеньев пользуясь положением в 3.2: Определить силы инерции звеньев:
,
,
,
,
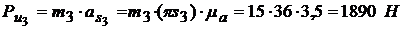где 
- берется из кинематического анализа механизма (рис3.12. б).
2. Определить на схеме механизма точки приложения и направления силы инерции звеньев:
Силы инерции звеньев 5 и 4
1. через точку Е проводим линию çê 
и укажем направление силы инерции 5 звена 
противоположно вектору (рис.3.12. а);
2. 
через точку S4 проводим линию 1 çê 
;
3. находим точку качения К шатуна 4 по формуле:
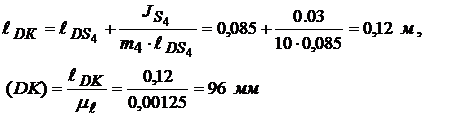
4. через точку К проводим линию 2 çê 
;
5. 
через точку Т пересечения линии 1 и 2 проводим линию 3 çê 
и укажем направление силы инерции 4 звена 
противоположно вектору (рис.3.12. а).
