2018-03-09
112
1. Повторите основные определения; формулы и правила вычисления интеграла; разберите примеры
2. Подберите для каждого задания соответствующие формулы и правила
Определение 1. Первообразной функцией для данной функции 
называется такая функция 
, производная которой равна , т.е. 
.
Например, первообразной функцией для функции 
является 
, т.к.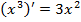 
. Но эта первообразная не единственная, а только одна из многих, т.к. функции все функции вида 
, где С – произвольная постоянная, являются первообразными для 
, поскольку 
.
Действительно, если на некотором промежутке функция является первообразной для функции , то для этой последней будет первообразной и любая функция вида 
, где С – постоянная.
Определение 2. Если – какая-либо первообразная функция для , то выражение , где С – произвольная постоянная, называется неопределенным интегралом от функции и обозначается символом 
.
При этом функция называется подынтегральной функцией, а выражение 
называется подынтегральным выражением, а знак 
называется знаком интеграла.
|
|
|
Согласно определению неопределенного интеграла, можно записать
Операция нахождения первообразной по данной функции называется интегрированием.
Пример 1. Найти: 1) 
; 2) 
.
Решение.
1) Функция 
производная функции 
. Следовательно,
2) Функция 
производная функции 
. Следовательно, 
Свойства неопределенного интеграла
1. 
2. 
3. 
4. 
Таблица неопределенных интегралов
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
|
Методы интегрирования
1. Непосредственное интегрирование
Непосредственным интегрированием принято называть вычисление неопределенных интегралов путем приведения их к табличным с применением основных свойств.
Пример 2. Найти 
.
Решение. 
.
2. Метод замены переменных
Метод замены переменных заключается в преобразовании интеграла 
в интеграл 
, который легко вычисляется по какой-либо из табличных формул интегрирования.
Одним из вариантов метода замены переменной является способ подведения под знак дифференциала, заключающийся в преобразовании:
.
Пример 3. 
Решение. 
.
Пример 4. Найти интеграл методом замены переменной:
1) 
; 2) 
Решение.
1) 
.
2) 
.
При помощи подстановок 
нетрудно вычислить следующие интегралы:
| 
|
| 
|
| 
|
|
Фигура, ограниченная графиком не прерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией.
Ее площадь вычисляетс по формуле Ньютона-Лейбница:
Если криволинейная трапеция расположена по осью абсцисс и ограничена ею, то площадь находится по формуле:
Вопросы для самоконтроля:
|
|
|
1. Какая функция называется первообразной?
2. Как обозначается первообразная?
3. Как обозначается множество первообразных?
4. Перечислите свойства неопределенных интегралов.
5. Перечислите методы интегрирования.
6. Каков геометрический смысл пределов интегрирования?
