Методические указания по выполнению практической работы

1. Повторите определение и алгоритм решения ДУ с разделяющимися переменными; выполните задание № 1

2. Выполните задание № 2, используя формулу для общего решения ЛДУ

3. Повторите определение ЛДУ второй степени и методы его решения; разберите примеры; выполните задание № 3

4. Проработайте алгоритм нахождения частного решения ЛДУ второй степени (задача Коши); выполните задание № 4

Определение 1. Дифференциальное уравнение вида y´+py=q, где p и q – действительные числа, называется линейным степени.

Если q=0, то уравнение является однородным. Однородное ЛДУ решается как уравнение с разделяющимися переменными.

Общее решение неоднородного ЛДУ имеет вид:

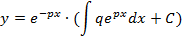
Определение 2. Уравнение y´´+py´+q=f(x), где p и q – постоянные действительные числа, а f(x) – заданная непрерывная функция, называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.

Если f(x)=0, то общее решение дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

y=C₁y₁+C₂y₂,

где С₁ и C₂ – произвольные постоянные, y₁ и y₂ – два линейно-независимых частных решения исходного уравнения.

Чтобы найти частные решения составляется характеристическое уравнение

                                          k²+pk+q=0.

Тогда y₁ = 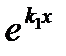, y₂ = 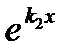. Общее решение примет вид:

                                          y=C₁ 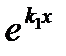+ C₂ .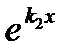

Пример 1. Решить дифференциальное уравнение y´´-2y´-3=0.

       Составляем характеристическое уравнение k²-2k-3=0. Корнями характеристического уравнения являются k₁=3 и k₂= - 1. Тогда частные решения примут вид y₁=e^3x, y₂=e^-x. Общим решением исходного дифференциального уравнения второго порядка является

                                                      y=C₁e^3x+C₂e^-x.

       В приведенном примере k₁ и k₂ различные действительные значения.

       Пусть k₁ и k₂ действительные, но равные значения. Тогда одно частное решение будет иметь вид y₁=e^kx, в качестве второго частного решения можно взять функцию y₂=xe^kx. Общее решение выглядит так: y=e^kx(C₁+C₂x).

       Пусть k₁ и k₂ – комплексные числа. k₁=a+bi, k₂=a-bi. Тогда частные решения имеют вид y₁=e^(a+bi)x, y₂=e^(a-bi)x. Общее решение примет вид

                                                      y=e^ax(C₁ ∙cosbx+C₂ ∙sinbx).

Пример 2. Решить дифференциальное уравнение y´´-4y´+13y=0.

       Составляем характеристическое уравнение:

k²-4k+13=0,

D=(-4)²-4∙1∙13= -36, так как D<0, то корни являются комплексными числами. Представим дискриминант следующим образом: D=36i², тогда k_1,2= 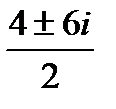, k_1,2=2±3i. Значит, действительная часть комплексного числа a=2, мнимая часть b=3.

Имеем следующее общее решение исходного дифференциального уравнения: y=e^2x(C₁∙cos3x+C₂∙sin3x).

       Если в дифференциальном уравнении второго порядка с постоянными коэффициентами вида y´´+py´+q=f(x), f(x)≠0, то данное уравнение является неоднородным.

       Общим решением линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами является сумма любого частного его решения (y^*) и общего решения соответствующего однородного уравнения (y_о). Частное решение можно найти по виду правой части.

Существуют правила для отыскания частных решений. Обозначим частное решение y^*.

I. Если f(x)=ax²+bx+c, то y^*=Ax²+Bx+C. Если корнем характеристического уравнения является 0, то y^*=x^k(Ax²+Bx+C).

II. Если f(x)=ae^αx, то y^*=Ae^αx. Если α кратный корень характеристического уравнения, то y^*=Ax^ke^αx.

III. Если f(x)=acosβx+bsinβx, то y^*=Acosβx+Bsinβx. Если ±βi являются корнями характеристического уравнения, то y^*=x(Acosβx+Bsinβx).

 

Примеры решения линейных неоднородных дифференциальных уравнений

 

а) y´´-2y´+y=x+1

Рассмотрим соответствующее однородное уравнение y´´-2y´+y=0. Составим характеристическое уравнение k²-2k+1=0. Имеем два одинаковых корня k=1.

Общее решение однородного уравнения примет вид y_о= e^x(C₁+C₂x).

Найдем частное решение неоднородного уравнения. Согласно первому правилу частное решение имеет вид y^*=Ax+B. Тогда (y^*)´=A, (y^*)´´=0. Подставим значения y^*, (y^*)´, (y^*)´´ в исходное уравнение

0-2A+Ax+B=x+1.

Сравнив коэффициенты справа и слева, находим A=1, B=3. Значит, y^*=x+3.

Таким образом, общим решением исходного уравнения будет

                   y=y_о+y^*=e^x(C₁+C₂x)+x+3.

 

б) y´´-4y´+3y=3e^2x

       Рассмотрим соответствующее однородное уравнение y´´-4y´+3y=0. Характеристическое уравнение k²-4k+3=0 имеет корни k₁=1, k₂=3. Общее решение однородного уравнения примет вид y_о=C₁e^x+C₂e^3x.

       Частное решение неоднородного уравнения будем искать в виде y^*=Ae^2x. Дважды продифференцируем, будем иметь (y^*)´=2Ae^2x, (y^*)´´=4Ae^2x. Подставим значения y^*, (y^*)´, (y^*)´´ в исходное уравнение, получим

                   4Ae^2x-8Ae^2x+3Ae^2x=3e^2x,

                   -Ae^2x=3e^2x.

       Получим A=-3. Частным решением будет y^*=-3e^2x. Общим решением исходного уравнения будет

                              y=y_о+y^*=C₁e^x+C₂e^3x-3e^2x.

 

в) y´´+9y=5cos2x

       Рассмотрим соответствующее однородное уравнение y´´+9y=0. Корнями характеристического уравнения являются k₁=3i, k₂=-3i. Общим решением является y_о=C₁cos3x+C₂sin3x.

       Частное решение будем искать в виде y^*=Acos2x+Bsin2x. Тогда

(y^*)´=-2Asin2x+2Bcos2x, (y^*)´´=-4Acos2x-4Bsin2x.

Подставим значения y^*, (y^*)´, (y^*)´´ в исходное уравнение, получим

                   -4Acos2x-4Bsin2x+9Acos2x+9Bsin2x=5cos2x.

       Сравнив коэффициенты справа и слева, получим A=1,B=0. Значит, частным решением неоднородного уравнения будет являться y^*=cos2x. Общее решение примет вид

                              y= y_о+y^*=C₁cos3x+C₂sin3x+cos2x.

Вопросы для самоконтроля:

1. Какое уравнение называют дифференциальным уравнением первого (второго) порядка?

2. Какой вид имеет общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами?

3. Какой вид имеет общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?

4. В чем заключается задача Коши?