Пусть имеется одиночный импульс s(t).

Мысленно (пунктиром) осуществим периодическое повторение этого импульса с периодом Т, для этой периодической последовательности запишем:
 (1)
(1)
 (2)
(2)
Подставим (2) в (1), получим:
 (3)
(3)
Выражение (3) справедливо для нашего импульса лишь на интервале от 0 до Т. При Т →∞, Ω→dω, kΩ→ω, получим:
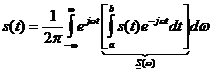
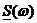 – спектральная характеристика импульсного колебания.
– спектральная характеристика импульсного колебания.
 (4) – прямое преобразование Фурье,
(4) – прямое преобразование Фурье,
 (5) – обратное преобразование Фурье.
(5) – обратное преобразование Фурье.
Вместо (4) и (5) договорились писать условное обозначение:
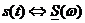
Спектральная характеристика в общем случае комплексная функция, а значит у нее есть модуль и аргумент, то есть  .
.
Выясним физический смысл спектральной характеристики и ее модуля. Сравним выражения (5) и (1):
 (5)
(5)
 (1)
(1)
 и
и 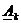 имеют один и тот же смысл.
имеют один и тот же смысл.
 – комплексная амплитуда гармоники с частотой ω.
– комплексная амплитуда гармоники с частотой ω.
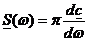 (6)
(6)
 (7) – модуль спектральной характеристики, имеет смысл спектральной плотности амплитуд, его принято называть амплитудным спектром импульса.
(7) – модуль спектральной характеристики, имеет смысл спектральной плотности амплитуд, его принято называть амплитудным спектром импульса.
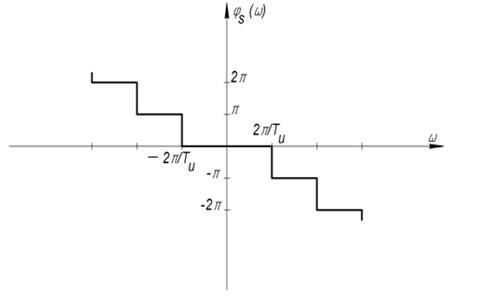
 – фазовый спектр; в отличие от спектров периодического колебания спектры импульсного колебания являются непрерывными, сплошными.
– фазовый спектр; в отличие от спектров периодического колебания спектры импульсного колебания являются непрерывными, сплошными.
Пример: найдем спектральную характеристику импульса
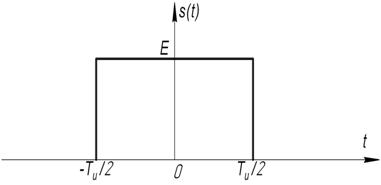
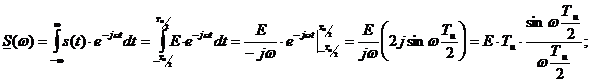

В состав импульсного колебания могут входить гармоники с любыми частотами.
Найдем связь спектра импульсного колебания (одиночного импульса) и спектра периодической последовательности таких импульсов. Для этого сопоставим выражения (2) и (4)
 (2)
(2)
 (4)
(4)
Можно сказать:
 (8)
(8)
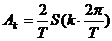 (9)
(9)
 (10)
(10)
Из выражения (10) следует, что модуль спектральной характеристики одиночного импульса и огибающая дискретного амплитудного спектра периодической последовательности этих импульсов, совпадают по форме и отличаются лишь масштабным коэффициентом 1/Т.
|

Проверим это на примере последовательности прямоугольных импульсов.
Пример:
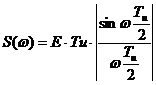

 2018-03-09
2018-03-09 162
162








