Преобразуем известное разложение в ряд Фурье по тригонометрическим функциям:
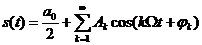 (1)
(1)
где  ;
;
Известно, что:
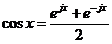 (2)
(2)
С учетом (2) получим:
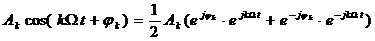
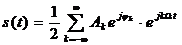
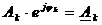 – комплексная амплитуда k-ой гармонической составляющей.
– комплексная амплитуда k-ой гармонической составляющей.
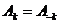
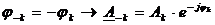
Представление колебания рядом Фурье в комплексной форме:
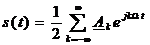 (3)
(3)
При таком представлении считается, что в состав колебания входят гармоники с положительными и отрицательными частотами. 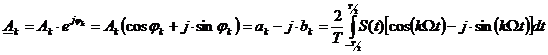

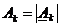
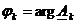
При комплексном представлении ряда Фурье, амплитудные и фазовые спектры периодического колебания становятся двухсторонними. Амплитуды гармоник с частотами kΩ и - kΩ равны  .
.
На практике можно использовать и односторонние и двухсторонние спектры.
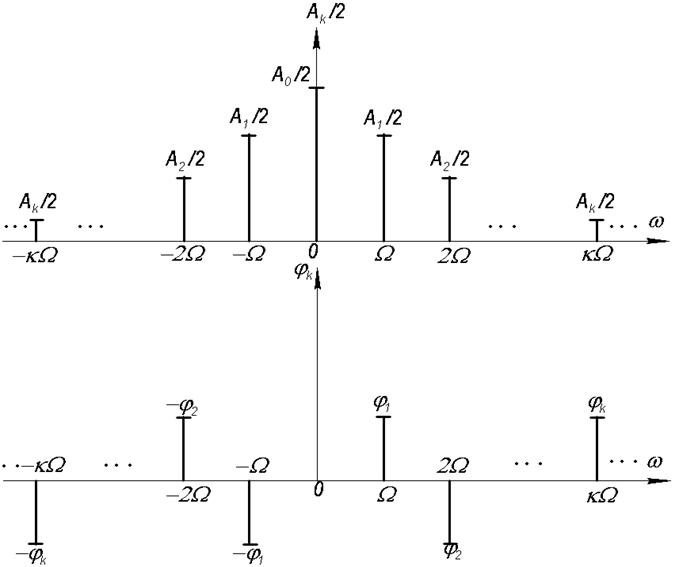
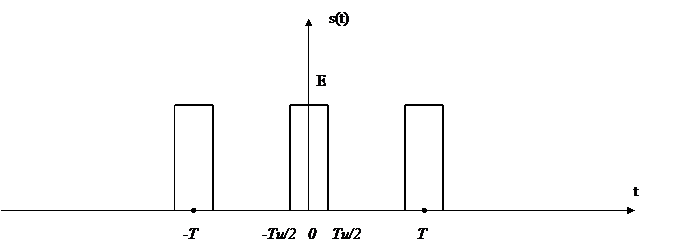
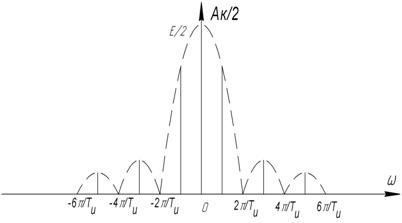
Пример:
 |

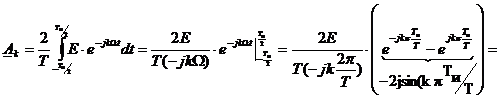
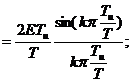
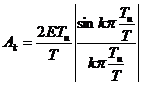
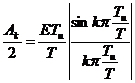
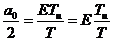 - среднее значение (постоянная составляющая).
- среднее значение (постоянная составляющая).
1) Пусть период 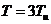
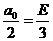
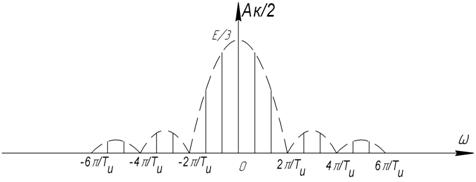
2) 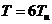


3) 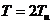
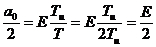
 2018-03-09
2018-03-09 99
99








