Соотношение между длительностью импульса и шириной его спектра

 

Это соотношение определяется 6-м свойством преобразования Фурье

Чем протяженнее сигнал во времени, тем менее протяжен его спектр. Однако само понятие протяженность сигнала во времени (длительность импульса) и протяженность спектра по частоте (ширина спектра) нуждается в уточнении.

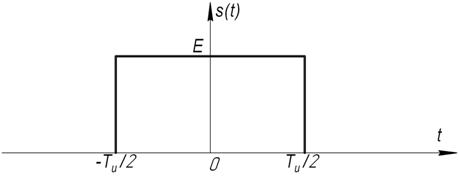
Начнем с длительности импульса. Есть импульсы (а) (например прямоугольный, треугольный…), у которых эти понятия определены. Но есть и такие (б), для которых это понятие не определено.

Чтобы получить единообразие в определении длительности импульсов используют энергетический метод, где вводят понятие активной длительности импульса ∆ t_{a .}

∆t_a – это интервал времени, в котором содержится бóльшая (основная) часть энергии импульса, например, 90%.

Если сигнал (импульс) начинается с нуля, то есть s(t)=0, t<0, то

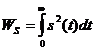
Пример: найти активную длительность прямоугольного импульса.

 

 

 

  Вводится также понятие активной ширины спектра импульса [∆ω_а] – интервал частот, в котором содержится основная или большая часть энергии импульса, например, 90% .

Если вычислить активную длительность импульса ∆ t_aи [∆ω_а] для импульсов различной формы, то выяснится общее для всех импульсов правило:

Как бы мы не изменяли форму импульса, всегда [∆f_а]^.∆t_a≥μ, где μ – некоторая постоянная.

 

§8 ^а Примеры вычисления спектральной характеристики некоторых импульсных сигналов.

1)

Ранее получено ,

 

2)

 

3.

 

 

 

,

.

 

 

4.

 

                   

 

                   

    

                

 

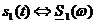
5. Функция Дирака (δ – импульс)

	0

s(t)

 

t

Свойства δ-импульса:

а)

б)

, где ε – бесконечная малая величина.

 

Найдем обратное преобразование Фурье:

 

6. Единичный скачок или функция Хевисайда.

s(t)

t

0

 

 

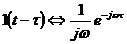
7. Гармоническое колебание.

---

---