Теорема. Для того чтобы числовой ряд  сходился, необходимо и достаточно, чтобы для произвольного ε > 0 нашелся номер N = N (ε) такой, что для всех n > N неравенство | аn + аn +1 + … + аn + p |< ε выполнялось для всех р = 0, 1, 2, …
сходился, необходимо и достаточно, чтобы для произвольного ε > 0 нашелся номер N = N (ε) такой, что для всех n > N неравенство | аn + аn +1 + … + аn + p |< ε выполнялось для всех р = 0, 1, 2, …
Пример 4. Исследовать на сходимость ряд  +
+  +
+  + … +
+ … +  +…
+…
• Используем критерий Коши: возьмем р = 2 n.
Имеем: | an + … + a 2 n |=  >
>  >
>  =
=  .
.
Критерий Коши не выполняется. Следовательно, ряд расходится.
Следствие. Так как для сходимости ряда неравенство | аn + аn +1 + … + аn + p |< ε должно выполняться для
всех р = 0, 1, 2, …, в т.ч. и для р = 0, то это означает, что, если ряд  сходится, то
сходится, то  аn = 0.
аn = 0.
Отсюда следует
Необходимый признак сходимости ряда
Если  аn отличен от нуля или не существует, то ряд
аn отличен от нуля или не существует, то ряд  расходится.
расходится.
Но если  аn = 0, то ряд может как сходиться, так и расходиться.
аn = 0, то ряд может как сходиться, так и расходиться.
Пример 5. Исследовать на сходимость ряд–1 + 0 +  +
+  + cos
+ cos  + … =
+ … =  .
.
• Используем необходимый признак сходимости: 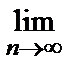 an =
an =  cos
cos  = cos 0 = 1 ≠ 0 => ряд расходится.
= cos 0 = 1 ≠ 0 => ряд расходится.
Пример 6. Исследовать на сходимость ряд1 +  +
+  +
+  + … =
+ … =  (гармонический ряд).
(гармонический ряд).
• Используем необходимый признак сходимости: 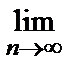 an =
an = 
 = 0, но гармоническийряд расходится.
= 0, но гармоническийряд расходится.
РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
Признак сравнения
Пусть даны два ряда а 1 + а 2 + а 3 + … + аn + … =  и b 1 + b 2 + b 3 + … + bn + … =
и b 1 + b 2 + b 3 + … + bn + … = 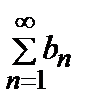 , члены которых аn и bn положительны. Если, начиная с некоторого номера N, для всех n > N выполняется неравенство аn ≤ bn, то из сходимости (большего) ряда
, члены которых аn и bn положительны. Если, начиная с некоторого номера N, для всех n > N выполняется неравенство аn ≤ bn, то из сходимости (большего) ряда 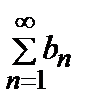 следует сходимость (меньшего) ряда
следует сходимость (меньшего) ряда  , а из расходимости (меньшего) ряда
, а из расходимости (меньшего) ряда  следует расходимость (большего) ряда
следует расходимость (большего) ряда 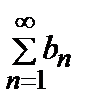 .
.
⃰ Составим частичные суммы данных рядов: Sn = а 1 + а 2 + а 3 + … + аn,  = b 1 + b 2 + b 3 + … + bn. Из условия теоремы следует, что Sn ≤
= b 1 + b 2 + b 3 + … + bn. Из условия теоремы следует, что Sn ≤ 
 n = 1, 2, …
n = 1, 2, …
1) Предположим, что ряд 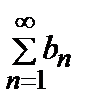 сходится, т.е. существует
сходится, т.е. существует 
 =
=  . Так как все члены данных
. Так как все члены данных
рядов положительны, то 0 ≤  ≤
≤  , откуда в силу того, что аn ≤ bn 0 ≤ Sn ≤
, откуда в силу того, что аn ≤ bn 0 ≤ Sn ≤ 
 n = 1, 2, …. Таким образом, все частичные суммы Sn ряда
n = 1, 2, …. Таким образом, все частичные суммы Sn ряда  ограничены и возрастают при возрастании n Следовательно, последовательность частичных сумм { Sn } является сходящейся, что означает сходимость ряда
ограничены и возрастают при возрастании n Следовательно, последовательность частичных сумм { Sn } является сходящейся, что означает сходимость ряда  . При этом, при переходе к пределу в неравенстве 0 ≤ Sn ≤
. При этом, при переходе к пределу в неравенстве 0 ≤ Sn ≤  при n →∞ получим, что 0 ≤ S ≤
при n →∞ получим, что 0 ≤ S ≤  , т.е. сумма S ряда
, т.е. сумма S ряда  не превосходит суммы
не превосходит суммы  сходящегося ряда
сходящегося ряда 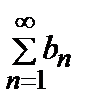 .
.
2) Пусть ряд  расходится. Так как все аn ≥ 0, то последовательность { Sn } возрастает и,
расходится. Так как все аn ≥ 0, то последовательность { Sn } возрастает и,
следовательно,  Sn = +∞. В силу неравенства
Sn = +∞. В силу неравенства  ≥ Sn (n = 1, 2, …) получаем
≥ Sn (n = 1, 2, …) получаем 
 = +∞, т.е.ряд
= +∞, т.е.ряд 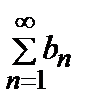 расходится.
расходится.
 2018-03-09
2018-03-09 263
263








